Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 – 20√3
=> F2A = 20(2 – √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

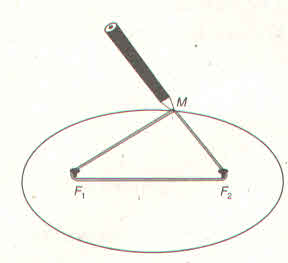
Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 - 20√3
=> F2A = 20(2 - √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

Từ giải thiết ta có: \(2a = 80 \Rightarrow a = 40,2b = 40 \Rightarrow b = 20\)
Suy ra, \(c = \sqrt {{a^2} - {b^2}} = 20\sqrt 3 \)
Suy ra vị trí đinh cách mép là \(a - c = 40 - 20\sqrt 3 = 5,36\) cm
Chiều dài vòng dây là \(2a + 2c = 2.40 + 2.20\sqrt 3 = 149,28\) cm
Vậy phải ghim hai cái đinh cách các mép tấm bìa 5,36 cm và lấy vòng dây có độ dài là 149,28 cm

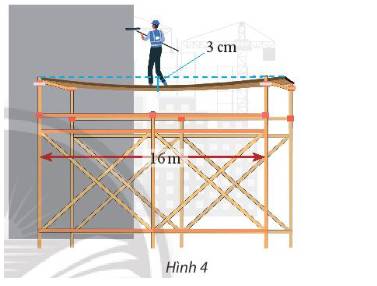
a) Ta vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
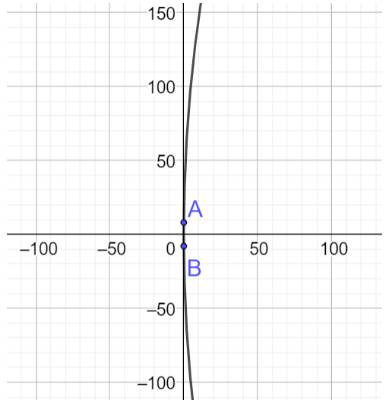
Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Từ giả thiết ta có: \(AB = 2{y_A} = 16 \Rightarrow {y_A} = 8 \Rightarrow A\left( {0,03;8} \right)\)
Thay tọa độ điểm A vào phương trình \({y^2} = 2px\)ta được \({8^2} = 2p.0,03 \Rightarrow p = \frac{{3200}}{3}\)
Vậy Phương trình chính tắc của parabol có dạng \({y^2} = \frac{{6400}}{3}x\)
b) Thay \(x = 1\)vào phương trình \({y^2} = \frac{{6400}}{3}x\) ta có \({y^2} = \frac{{6400}}{3}.1 \Rightarrow y = \frac{{80\sqrt 3 }}{3} \simeq 46,2\)
Vậy điểm có độ võng 1 cm cách tâm ván gỗ gần bằng 46,2 m
Chú ý khi giải: đổi về cùng đơn vị đo

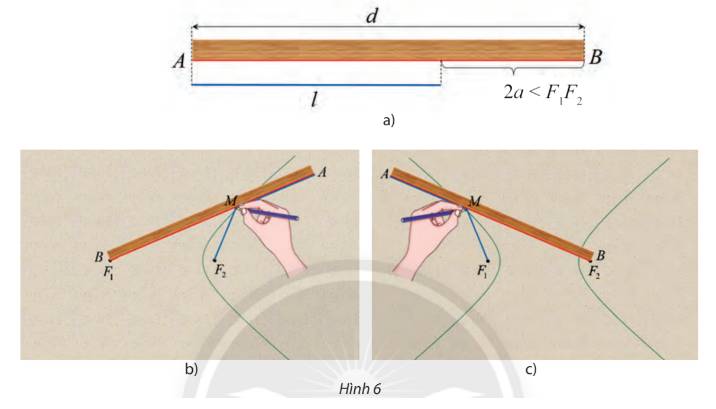
a) Khi điểm M trùng với điểm A ta có:
\(M{F_1} - M{F_2} = A{F_1} - A{F_2} = AB - A{F_2} = d - l = 2a\)
b) Tương tự khi điểm M trùng với điểm A ta có:
\(M{F_2} - M{F_1} = A{F_2} - A{F_1} = AB - A{F_1} = d - l = 2a\)

a) Chiều rộng của tấm bìa là \(\overline R = 170 \pm 2mm\), nghĩa là chiều rộng gần đúng \(R = 170\)với độ chính xác \(d = 2\)
Suy ra kích thước chiều rộng nằm trong khoảng \(\left[ {170 - 2;170 + 2} \right]\) hay \(\left[ {168;{\rm{ }}172} \right].\)
Tương tự, chiều dài của tấm bìa là \(\overline D = 240 \pm 2mm\)
Vậy kích thước chiều dài nằm trong khoảng \(\left[ {240 - 2;240 + 2} \right]\) hay \([238;242]\)
b) Chiều rộng gần đúng là 170 mm, chiều dài gần đúng là 240 mm.
Khi đó, diện tích tấm bìa là \(S = 170.240 = 40800\;(m{m^2})\)
Diện tích đúng, kí hiệu \(\overline S \), của tấm bìa trên thỏa mãn:
\(168.238 < \overline S < 172.242 \Leftrightarrow 39984 < \overline S < 41624\)
Do đó \(39984 - 40800 < \overline S - 40800 < 41624 - 40800\) hay \( - 816 < \overline S - S < 824 \Rightarrow \left| {\overline S - S} \right| < 824\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)
Cách 2:
Diện tích tấm bìa là:
\(\overline S = \left( {170 \pm 2} \right)\left( {240 \pm 2} \right) = 170.240 \pm \left( {170.2 + 240.2 + 2.2} \right) = 40800 \pm 824\left( {m{m^2}} \right)\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)

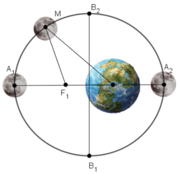
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km ⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km ⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.
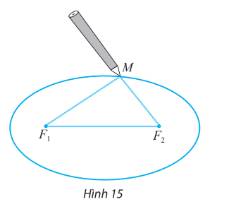

Giả sử Elip có phương trình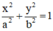
Độ dài trục lớn bằng 80cm ⇒ 2a = 80cm ⇒ a =40cm
Độ dài trục nhỏ bằng 40cm ⇒ 2b = 40cm ⇒ b = 20cm
Khi đó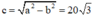 ⇒ F1F2 = 2c = 40√3 cm
⇒ F1F2 = 2c = 40√3 cm
Khoảng cách từ vị trí hai chiếc đinh F1, F2 đến hai mép là:
Độ dài vòng dây cuốn: MF1 + MF2 + F1F2 = 2a + 2c = 80 + 40√3 ≈ 149,3cm.