Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
R = |ZL – ZC| nên dòng điện lệch pha π 4 so với điện áp

Đáp án A
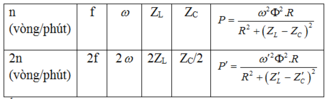
+ Khi tốc độ quay của roto là n (vòng/phút):


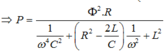
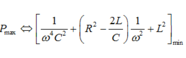
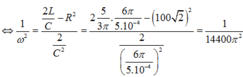
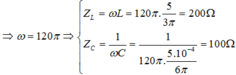
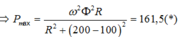
+ Khi tốc độ quay của roto là 2n (vòng/phút)
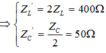
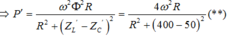
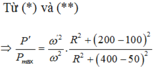
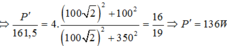

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Câu 1:
R thay đổi để PR max thì: \(R=\sqrt{r^2+(Z_L-Z_C)^2}=Z_{NB}\)
\(\Rightarrow U_R=U_{NB}=80\sqrt 3\) (V) (1)
\(U^2=(U_R+U_r)^2+(U_L-U_C)^2=240^2\) (2)
Và: \(U_{NB}^2=U_r^2+(U_L-U_C)^2=3.80^2\) (3)
Lấy (2) - (3) vế với vế ta có: \((U_R+2U_r).U_R=6.80^2\Rightarrow U_r=40\sqrt 3\)
Vậy hệ số công suất: \(\cos\varphi=\dfrac{U_r+U_R}{U}=\dfrac{\sqrt 3}{2}\)

Giải thích: Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R2 công suất tiêu thụ trên biến trở cực đại.
Khi đó ta có: R2 = |ZL - ZC | = 40 - 25 = 15W
Mặt khác: 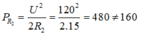
=> điều giả sử ban đầu là sai
=> Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r1 = 4W thì I1 = 0,1875
Theo định luật Ôm, ta có: 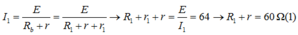
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos(100πt), R = R2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi ![]()
Mặt khác, ta có:
Công suất trên R2:
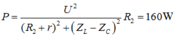
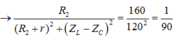
![]()
Kết hợp với (2) ta được: ![]()
Với r = 20W thay vào (1) => R1 = 60 - 20 = 40W
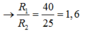

TH1: \(I_1=\frac{U}{Z}=\frac{U}{\sqrt{R^2+\left(Z_{:L}-Z_C\right)^2}}=3A.\)
TH2: Tụ C bị nối tắt tức là tụ chỉ là sợi dây dẫn và mạch chỉ còn RL
\(I_2=\frac{U}{Z}=\frac{U}{\sqrt{R^2+Z_L^2}}=3A.\)
=> \(I_1=I_2\Rightarrow Z_L=Z_C\).
Như vậy \(\cos\varphi_1=\frac{R_1}{Z_1}=1.\)
\(\varphi_u=\varphi_{i_1}=0\Rightarrow\varphi_2=\varphi_u-\varphi_{i2}=\frac{\pi}{3}.\)
=> \(\cos\varphi_2=\frac{1}{2}.\)
Chọn đáp án A.

Bài này thiếu dữ kiện thì phải, bạn xem lại xem còn thiếu gì không nhé.
bài này không thiếu dữ kiện đâu bạn minh coi kĩ đề rồi
Đáp án B