Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1.
Khoảng cách từ ảnh đến thấu kinh:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{d'}=\dfrac{1}{d}+\dfrac{1}{f}=\dfrac{1}{30}+\dfrac{1}{15}=\dfrac{1}{10}\)
\(\Rightarrow d'=10cm\)
Độ cao vật: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{18}=\dfrac{30}{10}\Rightarrow h=54cm\)
Câu 2.
Bạn tự vẽ hình nha!!!
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{60}=\dfrac{1}{d'}-\dfrac{1}{40}\Rightarrow d'=24cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{40}{24}\Rightarrow h'=1,2cm\)

a. Hình vẽ: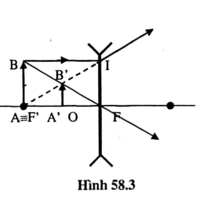
b. Ảnh ảo
c. Do A = F nên BO, AI là hai đường chéo của hình chữ nhật ABIO. B' là giao điểm của hai đường chéo BO, AI
=> A'B' là đường trung bình ΔABO
Nên OA' = 1/2.OA = 1/2.20= 10 (cm).

Vật sáng đặt ngoài tiêu cự vậy qua thấu kính hội tụ cho một ảnh thật, ngược chiều với vật như hình vẽ:
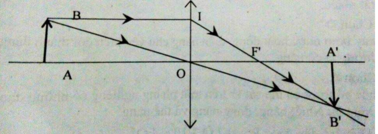
∆ ABO ~ ∆ A’B’O => AB/A'B' = OA/OA' (1)
∆ OIF’ ~ ∆ A’B’F’ => OI/A'B' = OF'/F'A' (2)
Và OI = AB nên từ (1) (2) suy ra:
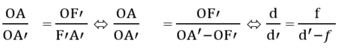
30/d' = 15/(d'-15 ) giải ra ta được d’ = 30cm. Vậy ảnh thật cách thấu kính 30cm.

Đáp án B
Tương tự từ ∆ đồng dạng ta được công thức:
d/d' = f/(f+d')
⇔ d/24 = 12/(12+24) = 1/3
d = 24/3 = 8 (cm)

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\)
\(\Rightarrow d'=4,8cm\)
Chọn câu B.
Vật AB cách thấu kính d = 30cm, vật ngoài khoảng OF nên cho ảnh thật ngược chiều với vật.
Trên hình vẽ, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được: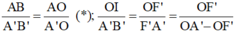
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
↔ dd' – df = d'f (1)dd' – df = d'f (1)
Chia cả hai vế của (1) cho tích d.d’.f ta được:
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 30cm, f = 15cm ta tính được: OA’ = d’ = 30cm