Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi trong mạch xảy ra cộng hưởng thì ω = ${\omega _0} = \dfrac{1}{{\sqrt {LC} }}$.

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Đáp án D
+ Khi ω 2 LC = 1 thì mạch có cộng hưởng ® Z = R ® U 0 = I 0 R .

Chọn C
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp với
cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện trong mạch là i 1 = I 0 cos ( ω t - π / 6 )
Mắc nối tiếp vào đoạn mạch này một tụ điện có điện dung C thì cường độ dòng điện trong mạch là i 1 = I 0 cos ( ω t + 2 π / 3 )
Vì đạt cùng điện áp hiệu dụng, mà giả thiết hai dòng điện có cùng giá trị hiệu dụng nên ta có tổng trở hai lần bằng nhau, tức là
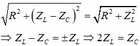
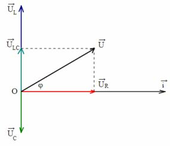
Phương trình u A B có dạng U 0 cos(wt+j)
Độ lêch trong trường hợp chưa ghép với tụ:
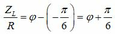
Độ lêch trong trường hợp có ghép với tụ:
![]()
![]()
![]()
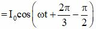
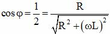
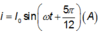
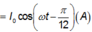
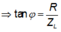
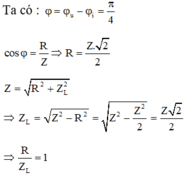
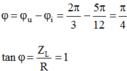

Đáp án B
+ Viết lại phương trình dòng điện là:
+