Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Có 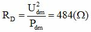
Ban đầu : 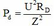
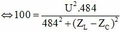 (1)
(1)
Sau khi nốt tắt tụ : 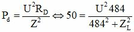 (2)
(2)
Chia (1) cho (2) được 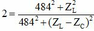
![]() (3)
(3)
Để có Zl thì pt (3) phải có nghiệm, tức là ![]()
![]()

Khi dung kháng là $100 \Omega$ thì công suất tiêu thụ của đoạn mạch là cực đại bằng 100 W nên
\(\begin{cases} Z_L=Z_{C_1}=100 \Omega \\ P=\dfrac{U^2}{R} =100 W \end{cases}\)
Khi dung kháng là $200 \Omega$ thì điện áp hiệu dụng giữa hai đầu tụ điện là $100\sqrt{2} V$ nên
$U_{C_2}=\dfrac{U.Z_{C_2}}{Z}=\dfrac{200.U}{\sqrt{R^2+(100-200)^2}}=100\sqrt{2}$
$\Rightarrow 2U^2=R^2+100^2$
$\Rightarrow 2.100.R =R^2 +100^2$
$\Rightarrow R=100 \Omega$

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Thay đổi L để công suất đạt giá trị lớn nhất \(\Rightarrow Z_L=Z_C=30\Omega\)
\(u_{RC}\) vuông pha với \(u_d\) \(\Rightarrow \tan\varphi_{RC}.\tan\varphi_d=-1\)
\(\Rightarrow \dfrac{-Z_C}{R}.\dfrac{Z_L}{r}=-1\)
\(\Rightarrow \dfrac{-30}{60}.\dfrac{30}{r}=-1\)
\(\Rightarrow r= 15\Omega\)
Công suất: \(P=\dfrac{U^2}{R+r}=\dfrac{180^2}{60+15}=432W\)
Chọn A


Đáp án C
Điện trở của bóng đèn :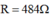
Lúc đầu
Điều kiện để phương trình trên có nghiệm là :
Vậy z L không thể có giá trị 274 Ω .