Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

y = 2x2 + 2mx + m -1 (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) m = 1 ⇒ y = 2x2 + 2x
Tập xác định D = R
\(\lim\limits_{x\rightarrow+\infty}y\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty\)
Bảng biến thiên:
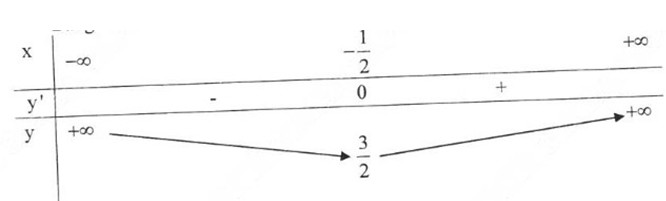
Đồ thị hàm số:
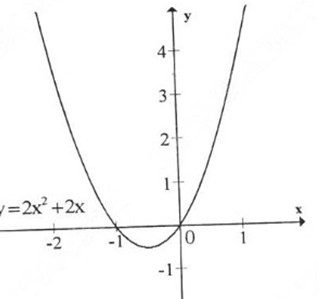
b) Tổng quát y = 2x2 + 2mx + m -1 có tập xác định D = R
y′=4x+2m=0⇔\(x=-\dfrac{m}{2}\).
Suy ra y’ > 0 với \(x>-\dfrac{m}{2}\) và \(y'< 0\) với \(x< -\dfrac{m}{2}\) tức là hàm số nghịch biến trên \(\left(-\infty;\dfrac{-m}{2}\right)\) và đồng biến trên \(\left(-\dfrac{m}{2};+\infty\right)\)
i) Để hàm số đồng biến trên khoảng (-1, +∞) thì phải có điều kiện (−1,+∞)∈(−\(\dfrac{m}{2}\),+∞)
Hay \(-\dfrac{m}{2}< -1\)\(\Leftrightarrow m>2\)
ii) Hàm số đạt cực trị tại \(x=\dfrac{m}{2}\)
Để hàm số đạt cực trị trong khoảng (-1, +∞), ta phải có:
\(-\dfrac{m}{2}\in\left(-1;+\infty\right)\) hay \(-\dfrac{m}{2}>-1\Leftrightarrow m< 2\).
c) (Cm) luôn cắt Ox tại hai điểm phân biệt
⇔ phương trình 2x2 + 2mx + m – 1 = 0 có hai nghiệm phân biệt.
Ta có:
Δ’ = m2 – 2m + 2 = (m-1)2 + 1 > 0 ∀m
Vậy (Cm) luôn cắt O x tại hai điểm phân biệt.

Cứ tăng giá thêm 100.000 ngàn đồng/tháng thì có 2 căn bỏ trống
--> Tăng thêm 100.000*n ngàn đồng/tháng thì sẽ có 2n căn bị bỏ trống
Gọi x = 2*10^{6} + 10^{5}*n là giá cho thuê để được thu nhập cao nhất
Suy ra thu nhập là y = x*(50 - 2n) (vì trong 50 căn đã có 2n căn bị bỏ trống)
y = x(50 - 2n) = (2*10^{6} + 10^{5}*n) (50 - 2n) = -2*10^{5}*n^{2} + 10^{6}*n + 10^{8}
= -2*10^{5} (n^{2} - 5n - 500) = -2*10^{5} [(n - 5/2)^{2} - 506,25] = -2*10^{5}(n - 5/2)^{2} + 1.0125 * 10^{8}
Thấy y đạt giá trị lớn nhất bằng 1.0125*10^{8} khi n = 2,5
Vậy giá thuê để đạt thu nhập lớn nhất là x = 2.000.000 + 100.000*2,5 = 2.250.000 đồng/tháng

a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0

Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.
 {
{ ) ∈ ∆ ⇔
) ∈ ∆ ⇔ 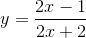 .
.
Chọn A
Phương pháp:
Gọi giá tua là x (triệu đồng).
Lập hàm số tổng doanh thu theo x.
Xét hàm tìm GTLN của hàm số trên và kết luận.
Cách giải:
Gọi x (triệu đồng) là giá tua.
Số tiền được giảm đi so với ban đầu là 2-x.
Số người tham gia được tăng thêm nếu bán với giá x là: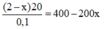
Số người sẽ tham gia nếu bán giá x là: 150 + (400-200x) = 550 - 220x
Tổng doanh thu là: f(x) = x(550-220x)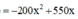
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy f(x) đạt giá trị lớn nhất khi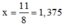
Vậy công ty cần đặt gói tua 1375000 đồng thì tổng doanh thu sẽ cao nhất là 378125000 đồng.