Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
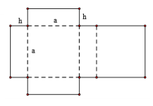
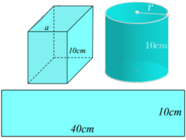
Thể tích khối hộp V = S h = h a 2
Diện tíc của tấm bìa là S b = 4 a h + 2 a 2 = 3 ⇔ h = 3 - 2 a 2 4 a 2
Từ 1 và 2 suy ra V = h a 2 = 3 - 2 a 2 4 a a 2 = a 3 - 2 a 2 4 ≤ 2 4 (khảo sát hàm số)
Dấu “=” xảy ra khi a = 1 2 ⇒ thế vào (2) ta được h = 2 2 ⇒ a + h = 2 .

Chọn A
Phương pháp: Sử dụng công thức thể tích hình trụ và công thức thể tích hình hộp.
Cách giải:


Yêu cầu bài toán thỏa mãn khi ta rút được 3 thẻ sao cho trong đó không có 2 thẻ nào là số tự nhiên liên tiếp
Số cách rút được 3 thẻ bất kì là C 26 3
Số cách rút được 3 thẻ có đúng 2 số tự nhiên liên tiếp:
Chọn 2 số tự nhiên liên tiếp: {1;2}{2;3}…{25;26}
TH1: Chọn 2 thẻ là {1;2} hoặc{25;26}: có 2 cách
Thẻ còn lại không được là 3 (hoặc 24): 26 -3 =23 (cách)
→ 2.23 =46 (cách)
TH2: Chọn 2 thẻ là: {2;3},{3;3},…{24;25}: 23 cách
Thẻ còn lại chỉ có: 26 -4 =22 (cách) →có 23.22 =506 (cách)
Số cách rút 3 thẻ trong đó có 3 số tự nhiên liên tiếp:
{1;2;3}{2;3;4}…{24;25;26}: 24 cách
Vậy có: C 26 3 - 46 - 506 - 24 = 2024 .
Chọn đáp án D.

Đáp án C
Gọi chiều dài đáy là x và chiều cao của hộp là y x ; y > 0 ; c m
Ta có
V = x 2 y = 180 ; S t p = 4 x y + 2 x 2 = 4.180 x + 2 x 2 = 360 x + 360 x + 2 x 2 ≥ 3 360 2 .2 3
Dấu “=” xảy ra
⇔ 360 x = 2 x 2 ⇔ x = 180 3 ⇒ y = 180 x 2 = 180 3 c m

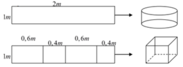
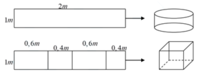
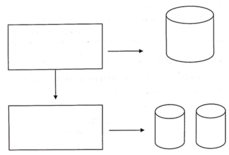
Ban đầu bán kính đáy là R, sau khi cắt và gò ta được 2 khối trụ có bán kính đáy là R 2 . Đường cao của các khối trụ không thay đổi. Ta có:
V 1 = S d h = π . R 2 . h V 2 = 2 S dl . h = 2 π R 2 h = πR 2 h 2
Khi đó: V 1 V 2 = 2
Đáp án C
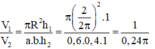



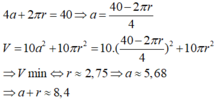
Chọn đáp án A