Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Điều chỉnh khoảng cách vật, thấu kính, màn chắn phù hợp để thu được ảnh thật từ một màn chắn.
- Đo các khoảng cách d, d' và ghi chép các số liệu.

Đáp án cần chọn là: D
Gọi d là khoảng cách từ vật đến thấu kính
d 1 ' là khoảng cách từ ảnh của vật qua thấu kính hội tụ đến thấu kính
d 2 ' là khoảng cách từ ảnh của vật qua thấu kính phân kì đến thấu kính
Ta có:
+ Khi dùng thấu kính hội tụ: 1 f = 1 d + 1 d 1 ' ⇔ 1 f = 1 d + 1 60 (1)
+ Khi dùng thấu kính phân kì: 1 − f = 1 d + 1 d 2 ' ⇔ 1 − f = 1 d + 1 − 12 (2)
Lấy (1) – (2) ta được:
2 f = 1 60 + 1 12 ⇒ f = 20 c m

Khoảng cách giữa thấu kính phân kì L và thấu kính hội tụ Lo phải lớn hơn tiêu cự của thấu kính hội tụ Lo
Vì ảnh cuối cùng của vật AB là ảnh thật, nên ảnh sẽ ngược chiều với vật, do đó số phóng đại của ảnh sau cùng phải nhỏ hơn 0 (k < 0 )
Mà 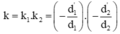
Vì 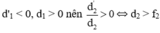
Gọi L là khoảng cách hai thấu kính ⇒ d2 = L - d'1 ⇔ L - d'1 > f2
Vì d'1 < 0 nên để đảm bảo L - d'1 > f2 thì L > f2
Vậy muốn ảnh cuối cùng của vật AB tạo bởi hệ thấu kính (L, Lo) bố trí như hình 35.2 là ảnh thật, thì khoảng cách giữa thấu kính phân kì L và thấu kính hội tụ Lo phải lớn hơn tiêu cự của thấu kính hội tụ Lo.


a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!

Sơ đồ tạo ảnh:

Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|
Vì vật thật, ảnh thật nên L = d + d'
Theo giả thiết có hai vị trí cho ảnh rõ nét trên màn. Gọi hai vị trí vật và ảnh tương ứng là


Đặt vật AB trước và gần thấu kính hội tụ L.
Điều chỉnh sao cho vật AB qua L0 cho ảnh nằm sau thấu kính phân kì L, thì sẽ thu được ảnh cuối cùng là ảnh thật.
∗ Các bước tiến hành:
– Giữ vật cố định, di chuyển thấu kính hội tụ và màn cho tới khi hứng được ảnh rõ nét trên màn (sắp xếp để thấu kính cho ảnh nhỏ).
– Đặt thấu kính phân kì trong khoảng giữa thấu kính hội tụ và màn, cách màn vài xăng-ti-mét, quan sát thấy ảnh trên màn bị nhòe đi. Gọi khoảng cách từ thấu kính phân kì đến màn lúc này là d2, đo d2.
– Di chuyển màn ra xa các thấu kính cho tới khi thu được ảnh rõ nét trên màn, đo khoảng cách d’2 từ thấu kính phân kì đến màn.
– tính tiêu cự f2 bằng công thức: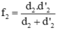
Vì d2 < 0 và │d’2│ > │d2│ nên f2 < 0