Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử đa diện (H) có m mặt. Vì mỗi mặt của (H) có 3 cạnh, nên m mặt có 3m cạnh. Nhưng mỗi cạnh của (H) là cạnh chung của đúng hai mặt nên số cạnh của (H) bằng c = \(\dfrac{3m}{2}\). Do c là số nguyên dương nên m phải là số chẵn. Ví dụ : Số cạnh của tứ diện bằng sáu.

Cho khối đa diện G có các đỉnh là ![]() lần lượt là số các mặt của H nhận chúng làm đỉnh chung. Tổng số các cạnh của G là:
lần lượt là số các mặt của H nhận chúng làm đỉnh chung. Tổng số các cạnh của G là:
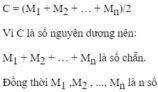
tự nhiên lẻ nên tổng của chúng là số chẵn khi n chẵn.
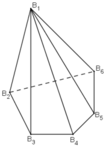
Ví dụ: Hình chóp ngũ giác ![]() là đỉnh chung của 5 mặt bên. Mỗi đỉnh
là đỉnh chung của 5 mặt bên. Mỗi đỉnh
B 1 , B 2 , B 3 , B 4 , B 5 , B 6 là đỉnh chung của ba mặt (hình trên).

Giả sử đa diện (H)(H) có các đỉnh là A1,…AdA1,…Ad, gọi m1,…mdm1,…md lần lượt là số các mặt của (H)(H) nhận chúng là đỉnh chung, ở đó m1,…mdm1,…md là những số lẻ.
Như vậy mỗi đỉnh AkAk có mkmk cạnh đi qua.
Ta có: đỉnh A1A1 có m1m1 cạnh đi qua.
đỉnh A2A2 có m2m2 cạnh đi qua.
...
đỉnh AdAd có mdmd cạnh đi qua.
Do đó số các cạnh (có thể trùng nhau) của đa diện là m1+m2+...+mdm1+m2+...+md.
Tuy nhiên, do mỗi cạnh là cạnh chung của đúng hai mặt nên số cạnh ở trên được đếm hai lần.
Vậy số cạnh thực tế của (H)(H) bằng
c=12(m1+m2+...+md)c=12(m1+m2+...+md)
Vì cc là số nguyên, m1,…mdm1,…md là những số lẻ nên dd phải là số chẵn.
Ví dụ : Hình chóp ngũ giác.
Đỉnh S là đỉnh chung của 5 mặt, tất cả các đỉnh còn lại là đỉnh chung của 3 mặt, hình chóp ngũ giác có 6 đỉnh
giup mình cày Sp vơi

Giả sử đa diện (H) có các đỉnh là A1, … Ad gọi m1, … md lần lượt là số các mặt của (H) nhận chúng là đỉnh chung. Như vậy mỗi đỉnh Ak có mk cạnh đi qua. Do mỗi cạnh của (H) là cạnh chung của đúng hai mặt nên tổng số các cạnh của H bằng
c=12(m1+m2+...+md)c=12(m1+m2+...+md)
Vì c là số nguyên, m1, … md là những số lẻ nên Đ phải là số chẵn. Ví dụ : Số đỉnh của hình chóp ngũ giác bằng sáu.

Ta có tứ diện đều ABCD, M là một điểm trong của nó. Gọi V là thể tích, S là diện tích mỗi mặt của tứ diện đều ABCD, h A , h B , h C , h D lần lượt là khoảng cách từ M đến các mặt (BCD), (CDA), (DAB), (ABC).
Khi đó ta có:
V = V MBCD + V MCDA + V MDAB + V MABCV
= S( h A + h B + h C + h D )/3
Từ đó suy ra h A + h B + h C + h D = 3V/S




* Gọi a là số cạnh, b là số mặt của khối đa diện.
Nếu khối đa diện có các mặt là tam giác thì mỗi mặt có ba cạnh. Trong ba cạnh đó mỗi cạnh lần lượt là cạnh chung của hai mặt.
Ta có 3b = 2a. Nghĩa là b chẵn.
Mà 2a chia hết cho 2 nên 3b cũng chia hết cho 2
⇒ b chia hết cho 2 hay b là số chẵn.
* Ví dụ: hình tứ diện đều có 4 mặt