Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Coi như a =1. Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B ⇒ Δ A B D cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ ( B C D ) và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ ( A H E ) ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có
A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 π

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án C
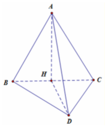
Gọi H là trung điểm của BC. Ta có: A H ⊥ B C
Mặt khác A B C ⊥ B C D ⇒ A H ⊥ B C D
Lại có A H = a 3 2 ⇒ V = 1 3 A H . S B C D = 1 3 . a 3 2 . a 2 3 4 = a 3 8

Đáp án B
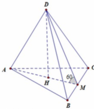
Gọi M là trung điểm của BC khi đó D M ⊥ B C A M ⊥ B C
Suy ra B C ⊥ ( D M A ) ⇒ D B C ; A B C ^ = 60 °
Lại có D M = A M = a 3 2
Dựng D H ⊥ A M ⇒ D H ⊥ ( A B C )
Khi đó V A B C D = 1 3 D H . S A B C = 1 3 D M . sin 60 ° . a 2 3 4 = a 2 3 16 .

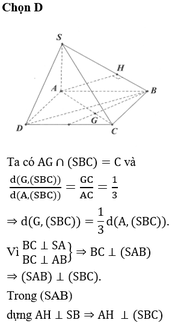





Đáp án A.
Gọi I là tâm mặt cầu ngoại tiếp ABCD ⇒ I ∈ Δ và I A = I B = R
Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất <=> IB nhỏ nhất
⇔ I B ⊥ Δ ⇔ I ≡ G ⇒ I A = I B = B G = a 3 3 = A G ⇒ V A B C D = 1 3 S B C D . A G = 1 3 . 1 2 . a . a 3 2 . a 3 3 = a 2 12