Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi M x ; y ; z ⇒ A M → = x − 1 ; y ; z + 3 , B M → = x + 3 ; y + 2 ; z + 5
Khi đó A M 2 + B M 2 = 30 ⇔ x − 1 2 + y 2 + z + 3 2 + x + 3 2 + y + 2 2 + z + 5 2 = 30
⇔ x − 1 2 + y + 1 2 + z + 4 2 = 9 ⇒ M ∈ S có tâm I − 1 ; − 1 ; − 4 , R = 3

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Chọn D.
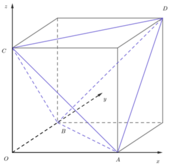
Phương pháp: Tứ diện ABCD có các cặp cạnh đối diện bằng nhau là tứ diện gần đều.
Cách giải: Theo giả thiết suy ra:
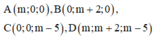
Theo tính chất của tứ diện gần đều tâm mặt cầu ngoại tiếp I của tứ diện ABCD là trung điểm OD
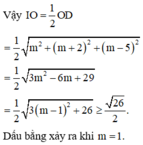



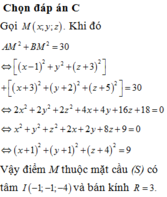

Đáp án B
* Gọi P, Q lần lượt là trung điểm của AB, CD. Theo giả thiết O là trung điểm của PQ nên suy ra O là trọng tâm của tứ diện ABCD.
M A → + M B → + M C → + M D → = a
⇔ 4 O M → = a ⇔ O M = a 4
Vậy tập hợp các điểm M trong không gian là mặt cầu tâm O bán kính r = a 4