Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

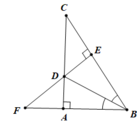
d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)

a) Hai tam giác = nhau theo trường hợp cạnh huyền góc nhọn (tự c/m)
b) Từ 2 tam giác = nhau ở phần a => AD= DE
Ta có tam giác ADF = tam giác EDC theo trường hợp góc cạnh góc (tự c/m)
=> DF= DC ( 2 cạnh tg ứng)
c) Xét tam giác ADF, có : góc A= 90 độ
=> DF là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện)
=> AD < DF
Mà DF= DC (chứng minh b)
=> AD < DC (đpcm)
b) Xét tam giác ADF và tam giác EDC, có:
Góc A= góc E (=90 độ)
AD= AE (vừa mình đã ns rồi)
Góc ADF= góc EDC (đối đỉnh)
Từ 3 điều trên => tam giác ADF = tam giác EDC (g-c-g)
=> DF= DC (2 cạnh tg ứng)

a. Hình vẽ (0.5 điểm)
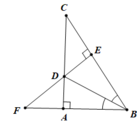
Xét ∆ABD và ∆EBD có:
∠(ABD) = ∠(DBE)
BD là cạnh chung
⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)

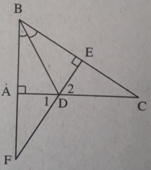
Xét ΔDAF và ΔDEC có:
DA = DE( chứng minh trên)
∠D1 = ∠D2 ( hai góc đối đỉnh)
∠DAF = ∠DEC = 90º
Suy ra: ΔDAF = ΔDEC (g.c.g) ⇒ DF = DC.

A B C E D F 1 2 1 2 1 2 1 2
Sửa đề: a) CMR : t/giác ABD = t/giác EBD; c) CMR: DC = DF
CM: a) Xét t/giác ABD và t/giác EBD
có: AB = BE (gt)
BD: chung
\(\widehat{B_1}=\widehat{B_2}\)(gt)
=> t/giác ABD = t/giác EBD (c.g.c)
b) Ta có: t/giác ABD = t/giác EBD (cmt)
=> \(\widehat{A_1}=\widehat{E_1}\)(2 góc t/ứng)
Mà \(\widehat{A_1}=90^0\) => \(\widehat{E_1}=90^0\)
=> DE \(\perp\)BC
c) Xét t/giác ADF và t/giác EDC
có: AD = DE (vì t/giác ABD = t/giác EBC)
\(\widehat{A_2}=\widehat{E_2}=90^0\)
\(\widehat{D_1}=\widehat{D_2}\)(đối đỉnh)
=> t/giác ADF = t/giác EDC (g.c.g)
=> DC = DF (2 cạnh t/ứng)

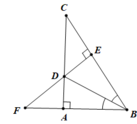
b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
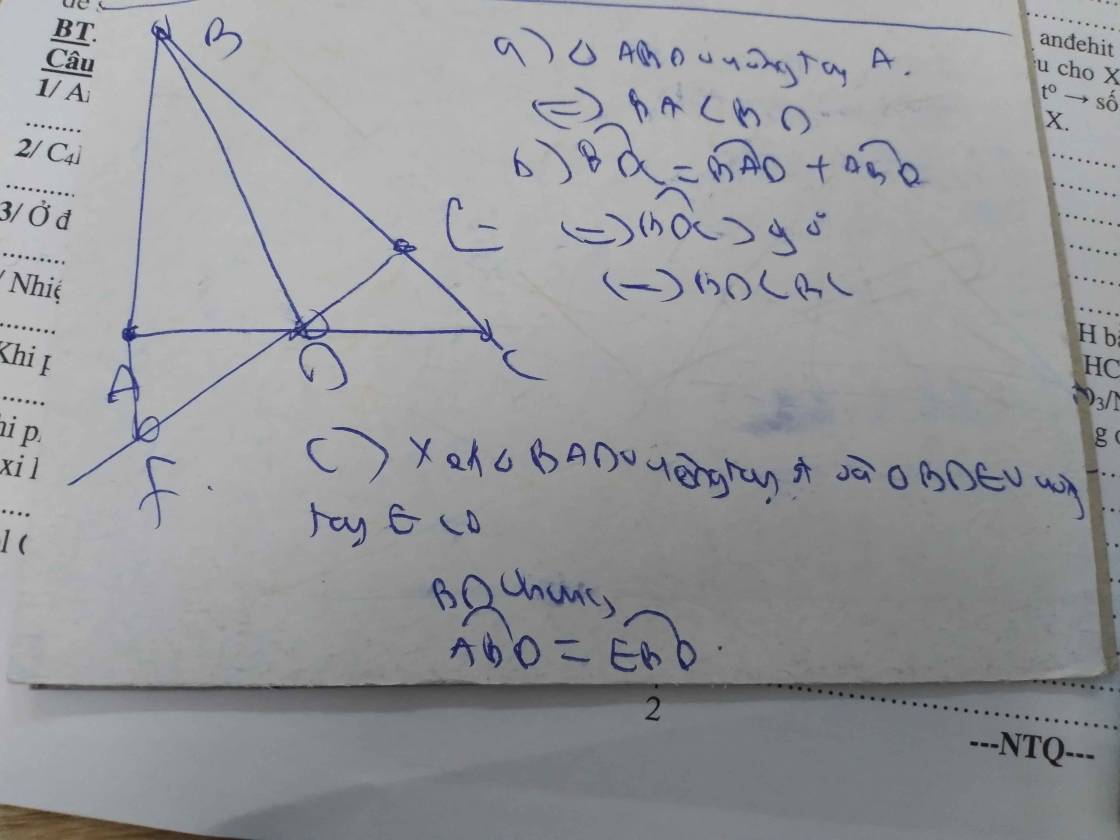

c. Xét ∆ADF và ∆EDC có:
AD = DE
∠(ADF) = ∠(EDC) (hai góc đối đỉnh)
⇒ ∆ADF = ∆EDC ( cạnh góc vuông – góc nhọn kề)(1 điểm)
⇒ DF = DC (hai cạnh tương ứng) (0.5 điểm)