
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



B2 : Hình dễ bạn tử kẻ hình nhá !
a)Ta có AH là đường cao
=> Góc AHB = AHC = 90o
Xết tam giác AHB có :
BAH + AHB + HBA = 180o ( tổng 3 góc trong 1 tam giác )
=> BAH + 90o + 70o =180o
=> BAH = 180o-70o-90o
=> BAH = 20o
Xét tam giác AHC cps :
AHC + HAC + HCA = 180o
=> 90 + HAC + 30 = 180
=> HAC = 180-30-90=60o
b) Ta có AD là đường phân giác
=> ABD= CAD = 80/2 = 40o
Xét tam giác ADB có :
ABD + BDA +DAB = 180
=> 70 + BDA + 40 = 180
=> BDA = 180-40-70 = 70
Xét tam giác ADC có :
ACD + CDA + DAC = 180
=> 30 + CDA + 40 = 180
=> CDA = 180-40-30
=> CDA=110
( **** )
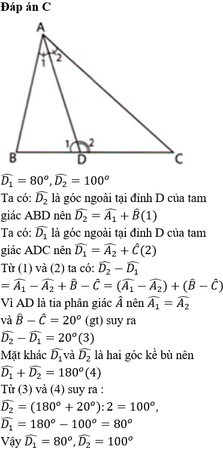
cho tam giác abc .co góc b-c= 20 độ .tia phân giác góc a cắt bc tại d .tính số đo của góc adc và adb


a,A+B+C=180 độ \(\Rightarrow C=30\)độ
\(\Rightarrow A>B>C\Rightarrow AB< AC< BC\)(t/c............)
b, t/gBAD=t/gBKD(c-g-c) suy ra DA=DK
c,BDC cân vì có DBC=DCB=30 độ
d, théo t/c của tam giác vuông (cạnh đối diện vs góc 30 độ =1/2 cạnh huyền)

a, xét tam giác ABD, tam giác HBD có
AB=BH ;góc ABD= góc HBD ( vì phân giác) ,BD chung
suy ra 2 tam giác bằng nhau theo trường hợp cạnh góc cạnh
b, vì 2 tam giác bằng nhau ( câu a) suy ra góc BAD= góc BDH mà BAD= 90 độ suy ra BHD =90 độ hay DH vuông góc với BC
C, nếu góc C =60 độ suy ra góc B = 0 độ suy ra góc ABD= 15 độ suy ra góc ADB = 90 độ -15 độ = 75 độ ( phụ nhau)

a) ta có: OE là đường trung trực của AC
mà E thuộc OE
=> EA = EC ( tính chất đường trung trực )
=> tam giác ACE cân tại E ( định lí tam giác cân)
Xét tam giác ABC
có: góc B = 100 độ
=> tam giác ABC là tam giác tù ( định lí)
b) Xét tam giác ABC
có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( định lí tổng 3 góc trong tam giác)
thay số: \(100^0+\widehat{B}+\widehat{C}=180^0\)
góc B + góc C = 180 độ - 100 độ
góc B + góc C = 80 độ (1)
ta có: OD là đường trung trực của AB
mà D thuộc OD
=> DA = DB ( tính chất đường trung trực)
=> tam giác ADB cân tại D ( định lí tam giác cân)
=> góc DAB = góc B ( định lí ) (2)
ta có: tam giác ACE cân tại E ( phần a)
=> góc CAE = góc C ( định lí)
Từ (1);(2);(3) => góc DAB + góc CAE = góc B + góc C = 80 độ
=> góc DAB + góc CAE = 80 độ
mà góc DAB + góc CAE + góc EAD = góc A
thay số: 80 độ + góc EAD = 100 độ
góc EAD = 100 độ - 80 độ
góc EAD = 20 độ
c) ta có: góc DAB = góc B ( cmt)
góc CAE = góc E ( cmt) (1)
Xét tam giác ABC
Có: OD cắt OE tại O
mà OD là đường trung trực của AB
OE là đường trung trực của AC
=> OA = OB = OC ( tính chất 3 đương trung trực trong tam giác)
vậy OA = OB
=> tam giác AOB cân tại O ( đinh lí tam giác cân)
=> góc OAB = góc OBA ( định lí) (2)
vậy OA = OC
=> tam giác AOC cân tại O ( định lí tam giác cân)
=> góc OAC = góc OCA ( định lí) (3)
vậy OB = OC
=> tam giác OBC cân tại O ( định lí tam giác cân)
=> góc OBC = góc OCB ( định lí) (4)
Từ (1);(2);(3);(4) => góc C + góc OCB = góc B + góc OBC ( = góc OAC = góc OBA)
góc CAE + góc OCB = góc DAB + góc OBC
=> góc CAE = góc DAB
mà góc CAE + góc EAO = góc DAB + góc DAO ( = góc OAC = góc OBA)
=> góc EAO = góc DAO
=> AO là tia phân giác góc DAE ( định lí)

a, Chứng minh tam giác ADB=tam giác ADC
=>góc BAD=góc CAD=>AD là tia phân giác của góc BAC=>góc BAD=góc CAD=10độ
b, Do tam giác ABC cân tại A và tam giác DCB đều nên góc ABC=(180độ-20độ):2= 80độ;góc DBC= 60độ
=> góc ABD=80 độ - 60 độ=20độ
Tia BM là tia phân giác của góc ABD=> góc ABM=góc DBM=10độ
Chứng minh được tam giác ABM = tam giác BAD(g.c.g) => AM=BD mà BD =BC nên AM=BC (đpcm)

a) Gọi số đo góc C là x (độ) (0<x<70). => Số đo góc B là x + 40 (độ).
Tổng 3 góc trong 1 tam giác là 180 độ. => Số đo góc A là 180 - (x + 40) - x = 140 - 2x (độ).
AM phân giác góc BAC. => Số đo góc BAM = Số đo góc CAM = (140 - 2x) : 2 = 70 - x (độ).
Tổng 3 góc trong tam giác AMC là 180 độ. => Số đo góc AMC = 180 - Số đo góc CAM - Số đo góc C = 180 - (70 - x) - x = 110 (độ).
Đáp số: Số đo góc AMC = 110 độ.
b) D là trung điểm BC, ED vuông góc với BC. => Tam giác EBC cân tại E. => Số đo góc EBC = Số đo góc ECB = x (độ).
Mà số đo góc ABC là (x + 40) (độ). => Số đo góc ABE = Số đo góc ABC - Số đo góc EBC = (x + 40) - x = 40 (độ).
Đáp số: Số đo góc ABE = 40 độ.
A B C M D E