Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

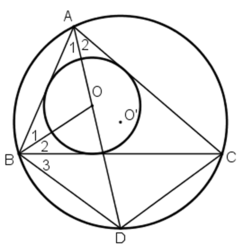
Do O là tâm đường tròn nội tiếp tam giác ABC nên O là giao điểm của ba đường phân giác của tam giác ABC.

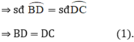
(hai cung bằng nhau căng hai dây bằng nhau).
+ 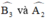 đều là các góc nội tiếp chắn
đều là các góc nội tiếp chắn 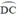
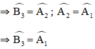
ΔOAB có 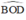 là góc ngoài của tam giác
là góc ngoài của tam giác

Từ (1) và (2) suy ra DB = DC = DO.
Vậy chọn đáp án D.

Hướng dẫn làm bài:
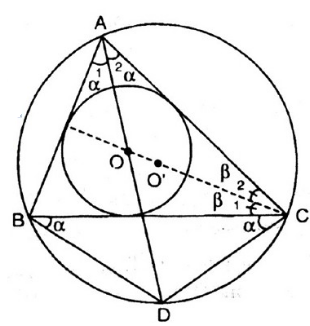
Vì AC vad BC tiếp xúc với đường tròn (O), AD đi qua O nên ta có:
ˆCAD=ˆBAD=αCAD^=BAD^=α (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)
⇒ cung CD = cung DB ⇒CD = DB (*)
Tương tự, CO là tia phân giác của góc C nên:
ˆACO=ˆBCO=βACO^=BCO^=β
Mặt khác: ˆDCO=ˆDCB+ˆBCO=α+β(1)(doˆBAD=ˆBCDDCO^=DCB^+BCO^=α+β(1)(doBAD^=BCD^
Ta có: ˆCODCOD^ là góc ngoài của ∆ AOC nên
ˆCOD=ˆOAC+ˆOCA=β+α(2)COD^=OAC^+OCA^=β+α(2)
Từ (1) và (2) ta có: ˆOCD=ˆCODOCD^=COD^
Vậy ∆DOC cân tại D (**)
Từ (*) và (**) suy ra CD = OD = BD
Chọn đáp án D

a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)

M A B C I D N O H K
a) CM: \(\widehat{OBM}=\widehat{ODC}\)
\(\widehat{OBM}+\widehat{OBC}=180^o\)( kề bù)
\(\widehat{ODC}+\widehat{OBC}=180^o\)( tứ giác ODCB nội tiếp )
=> \(\widehat{OBM}=\widehat{ODC}\)
b)
+)Xét tam giác MCN có CO là tia phân giác đồng thời là đường cao
=> Tam giác CMN cân tại C (1)
=> \(\widehat{BMA}=\widehat{DNA}=\widehat{BAM}\)( CD//BA => DN//BA)
=> Tam giác BMA cân tại B
=> BM=BA=CD ( ABCD là hình bình hành) (2)
+) CO là phân giác \(\widehat{BCD}\)
=> \(\widebat{BO}=\widebat{DO}\)
=> BO=DO (3)
+) Xét tam giác BOM và tam giác DOC có:
\(\widehat{OBM}=\widehat{ODC}\)( theo a)
BM=CD ( theo 2)
BO=DO (theo 3)
=> \(\Delta BOM=\Delta DOC\)
+) OM=OC
Và từ (1) => CO là đường trung trực của MN
=> OM=ON
Vậy OM=ON=OC
=> O là tâm đường tròn ngoại tiếp tam giác CMN
c) GỌi H là giao của IO và BD
=> IH vuông BD và H là trung điể m BD
Ta có: \(KD^2=\left(HD-HK\right)^2=HD^2+HK^2-2.HD.HK=ID^2-IH^2+IK^2-IH^2-2HD\left(HD-KD\right)\)
\(=ID^2+IK^2-2\left(IH^2+HD^2\right)+2HD.KD=ID^2+IK^2-2ID^2+2HD.KD\)
\(=IK^2-ID^2+2HD.KD\)
=> \(IB^2-IK^2=ID^2-IK^2=2HD.KD-KD^2\)
=> \(\frac{IB^2-IK^2}{KD^2}=\frac{2HD-KD}{KD}=\frac{BD-KD}{KD}=\frac{BK}{KD}\)(4)
Ta lại có: CK là phân giác trong của tam giác CBD
=> \(\frac{BK}{KD}=\frac{CB}{CD}\)
Và MB=DC ( theo cm câu a) , CM=CN ( Tam giác CMN cân)
=> CB=DN
=> \(\frac{BK}{KD}=\frac{DN}{MB}\)(5)
Từ (4), (5)
=> ĐPCM

Do O là tâm đường tròn nội tiếp tam giác ABC nên O là giao điểm của ba đường phân giác của tam giác ABC.
(hai cung bằng nhau căng hai dây bằng nhau).
+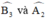 đều là các góc nội tiếp chắn
đều là các góc nội tiếp chắn 
ΔOAB có là góc ngoài của tam giác
là góc ngoài của tam giác
Từ (1) và (2) suy ra DB = DC = DO.
Vậy chọn đáp án D.