Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ MN//AC ~> N là trg điểm của AB và MN=1/2 AC
Gọi giao điểm của MN và BI là E
tam giác ABM có trọng tâm E nên EM=2/3 MN
~> EM=1/3 AC
Tam giác ADI=MEI ~> AD=ME ~> AD=1/3AC
chúc bạn học tốt
Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Xét ΔBEC có
M là trung điểm của BC
F là trung điểm của EC
Do đó: MF là đường trung bình của ΔBEC
Suy ra: MF//DE
Xét ΔAMF có
D là trung điểm của AM
DE//MF
Do đó: E là trung điểm của AF
Suy ra: AE=EF
mà EF=FC
nên AE=FE=FC
hay \(AE=\dfrac{EC}{2}\)

Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Gọi K là trung điểm của EC
Xét ΔBEC có
M là trung điểm của BC(gt)
K là trung điểm của EC(Gt)
Do đó: MK là đường trung bình của ΔBEC
Suy ra: MK//BE
hay MK//DE
Xét ΔAMK có
D là trung điểm của AM(Gt)
DE//MK(cmt)
Do đó: E là trung điểm của AK(Định lí 1 đường trung bình của tam giác)
Suy ra: AE=EK
mà EK=KC
nên AE=EK=KC
\(\Leftrightarrow AE=\dfrac{EK+KC}{2}=\dfrac{EC}{2}\)

Trên BE lấy N sao cho N là tr/đ BE.
Mà M là tr/đ BC
=> MN là đg tr/bình trong tam giác BEC
=> MN // EC và MN = 1/2 EC
Do MN // EC => góc EAD = gócDMN 2 góc so le trong
Dễ dàng cm đc tg AED = tg MND ( g.c.g )
=> AE =MN
Mà MN= 1/2 EC => AE = 1/2 EC
Từ M kẻ MK//DE ,MK cắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)
học tốt nhóe ~~~

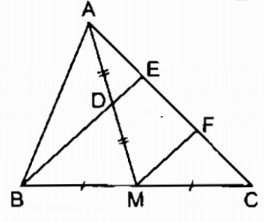
Gọi F là trung điểm của EC
Trong ∆ CBE ta có:
M là trung điểm của cạnh CB
F là trung điểm của cạnh CE
Nên MF là đường trung bình của ∆ CBE
⇒ MF // BE (tính chất đường trung bình của tam giác)
Hay DE // MF
Trong tam giác AMF ta có:
D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà EF=FC=\(\dfrac{EC}{2}\) nên AE=\(\dfrac{EC}{2}\)

Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Lời giải:
Áp dụng định lý Menelaus cho tam giác $AMC$ có $B,D,E$ thẳng hàng:
$\frac{BM}{BC}.\frac{DA}{DM}.\frac{EC}{EA}=1$
$\Leftrightarrow \frac{1}{2}.1.\frac{EC}{EA}=1$
$\Leftrightarrow EC=2EA$ hay $EA=\frac{1}{2}EC$ (đpcm)

A E F C M B
Qua M kẻ MF // AC , cắt AC tại F
Ta có : {MF//DEAD=DM{MF//DEAD=DM => DE là đường trung bình tam giác AMF => AE = EF (1)
Lại có : {MF//BEBM=MC{MF//BEBM=MC => MF là đường trung bình tam giác BEC => EF = FC (2)
Từ (1) và (2) suy ra AE = EF = FC => đpcm
Qua M kẻ MF // AC , cắt AC tại F
Ta có : {MF//DEAD=DM{MF//DEAD=DM => DE là đường trung bình tam giác AMF => AE = EF (1)
Lại có : {MF//BEBM=MC{MF//BEBM=MC => MF là đường trung bình tam giác BEC => EF = FC (2)
Từ (1) và (2) suy ra AE = EF = FC => đpcm

Gọi F là trung điểm của EC.
Trong ∆ CBE, ta có:
M là trung điểm của CB;
F là trung điểm của CE.
Nên MF là đường trung bình của ∆ CBE
⇒ MF// BE (tính chất đường trung bình của tam giác) hay DE// MF
* Trong ∆ AMF, ta có: D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà EF = FC = EC/2 nên AE = 1/2 EC