Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ∆ ABC đồng dạng với ∆ AMN nên:
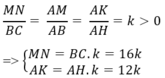
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
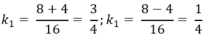
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
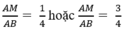

cái hình thì mk gửi link trong ib nhé
a) Gọi O là giao điểm của AC và BD
\(\Delta OAB\) vuông tại O có \(OA^2+OB^2=AB^2=49\)
Lại có: \(\tan BAC=\tan OAB=\frac{OB}{OA}=\frac{3}{4}\)\(\Leftrightarrow\)\(\frac{OA^2}{16}=\frac{OB^2}{9}=\frac{OA^2+OB^2}{16+9}=\frac{49}{25}\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{OA}{4}=\frac{7}{5}\\\frac{OB}{3}=\frac{7}{5}\end{cases}}\Leftrightarrow\hept{\begin{cases}OA=\frac{28}{5}\left(cm\right)\\OB=\frac{21}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}AC=2OA=\frac{56}{5}\left(cm\right)\\BD=2OB=\frac{42}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.\frac{56}{5}.\frac{42}{5}=\frac{1176}{25}=47,04\left(cm^2\right)\)
b) Gọi E, F lần lược là giao điểm của BD với MN và PQ
tam giác ABD có MQ // BD
\(\Rightarrow\)\(\frac{MQ}{BD}=\frac{MA}{AB}\) ( hệ quả định lí Talet )
tam giác OAD có QF // OA
\(\Rightarrow\)\(\frac{QF}{OA}=\frac{DQ}{AQ}=\frac{MB}{AB}\) ( hệ quả định lí Talet )
\(\Rightarrow\)\(\frac{MQ}{BD}+\frac{QF}{OA}=\frac{MA+MB}{AB}=1\)
\(\Rightarrow\)\(1\ge2\sqrt{\frac{MQ.QF}{BD.OA}}\)\(\Leftrightarrow\)\(MQ.QF\le\frac{1}{4}BD.OA\)
Tương tự, ta cũng có: \(NP.PF\le\frac{1}{4}BD.OC\)
\(\Rightarrow\)\(MQ.QF+NP.PF=S_{MEFQ}+S_{NEFP}=S_{MNPQ}\le\frac{1}{4}BD.AC=\frac{1}{2}S_{ABCD}=23,52\left(cm^2\right)\)
Dấu "=" xảy ra khi M, N, P, Q là trung điểm của AB, BC, CD, DA

đặt MA= x (cm)
tam giác ABC cân nên : 12-x
diện tích hình bình hành MNCP là : MP.MA = (12-x)x
diện tích bằng 32cm vuông , nê ta có phương trình:
x^2 -12x +32 = 0
giải pt ta được x1= 4 , x2 =8
vậy M cách A là 4cm hoặc 8cm.

4. Dễ thấy \(\Delta AML\approx\Delta LKC\left(g-g\right)\)
\(\Rightarrow\frac{AL}{LC}=\sqrt{\frac{S_{\Delta AML}}{S_{\Delta LKC}}}=\sqrt{\frac{42.7283}{51.4231}}\approx0.9115461896\)
\(\Rightarrow\frac{AL}{AC}=\frac{0.9115461896}{0.9115461896+1}=0.476863282\)
Lại có \(\Delta AML\approx\Delta ABC\left(g-g\right)\)
\(\Rightarrow\frac{S_{AML}}{S_{ABC}}=\left(\frac{AL}{AC}\right)^2=0.476863282^2=0.2273985897\)
\(\Rightarrow S_{\Delta ABC}=\frac{S_{\Delta AML}}{0.2273985897}=\frac{42.7283}{0.2273985897}\approx187.9\left(cm^2\right)\)
1. Ta có \(\frac{BH}{CH}=\frac{\sqrt{7}}{\sqrt{5}}\Rightarrow BH=\frac{\sqrt{7}}{\sqrt{5}}CH\)
Mặt khác \(BC=\sqrt{11}\Rightarrow BH+CH=11\)
\(\Rightarrow\frac{\sqrt{7}}{\sqrt{5}}CH+CH=11\)
\(\Leftrightarrow CH=\frac{-55+11\sqrt{35}}{2}\) và \(BH=\frac{77-11\sqrt{35}}{2}\)
Có BH, CH và BC tính đc AB, AC \(\left(AB=\sqrt{BH.BC};AC=\sqrt{CH.BC}\right)\)
Từ đó tính đc chu vi tam giác ABC.
2. Để cj gửi hình qua gmail cho
3. Chỉ còn cách làm từng bước thôi e
\(B=31+\frac{27}{\frac{30127}{2008}}=31+\frac{54216}{30127}=32+\frac{24089}{30127}\)
Để viết liên phân số, ta bấm phím tìm thương và số dư:
(Mỗi số b1, b2, b3, ..., bn-1 chính là thương; số chia của phép chia trước là số bị chia của phép chia sau, còn số dư của phép chia trước là số chia của phép chia sau, nhớ nhá)
- B1: Tìm thương và số dư của 30127 cho 24089, thương là 1, dư 6038, viết \(B=32+\frac{1}{1+...}\)
- B2: Tìm thương và số dư của 24089 cho 6038, thương là 3, dư 5975, viết \(B=32+\frac{1}{1+\frac{1}{3+...}}\)
- B3: Tìm thương và số dư của 6038 cho 5975, thương là 1, dư 63, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+...}}}\)
- B4: Tìm thương và số dư của 5975 cho 63, thương là 94, dư 53, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+...}}}}\)
...
Cứ làm như vậy, đến khi số dư là 1 thì dừng lại, phân số cuối cùng \(\frac{1}{b_n}\) thì bn chính là số chia cuối cùng, bn = 3
Kết quả: \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+\frac{1}{1+\frac{1}{5+\frac{1}{3+\frac{1}{3}}}}}}}}\)
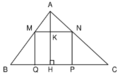

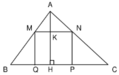


Vì ∆ ABC đồng dạng với ∆ AMN nên:
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn: