Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)

Kẻ BH vuông góc với AC
Xét ΔABH vuông tại H có \(BH=AB\cdot\sin A\simeq1,7101\left(cm\right)\)
\(S_{ABC}=\dfrac{BH\cdot AC}{2}=6.8404\left(cm^2\right)\)

Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos30^0=4\sqrt{3}\simeq6,928\left(cm\right)\)

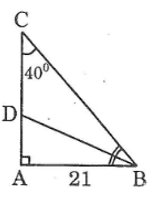
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

A B C H 35 50 o 60 o
Ta có \(CH=AC.cos\widehat{C}=35.cos50^o\)
\(AH=AC.sin\widehat{C}=35.sin50^o\)
\(BH=AH.cot\widehat{B}=35.sin50^o.cot60^o\)
\(\Rightarrow BC=BH+CH=35.cos50^o+35.sin50^o.cot60^o\)
\(\Rightarrow S_{ABC}=\frac{AH.BC}{2}=\frac{35.sin50^o\left(35.cos50^o+35.sin50^o.cot60^o\right)}{2}\)

A B C H
trong tam giac AHC co \(AH=AC\cdot\sin C=35\cdot\sin50\approx26,8\)
ap dung dl pitago vao AHC ta tinh dc \(HC=AC^2-AH^2\approx22,5\)
tg tu trong tam giac ABH co \(BH=\cot60\cdot26,8\approx15,5\)
\(\Rightarrow BC=BH+CH=38\)
\(\Rightarrow SABC=\frac{1}{2}BC\cdot AH=509,2\)
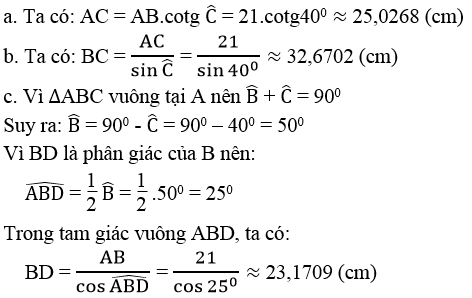


Kẻ AH ⊥ BC, tại H . Áp dụng hệ thức giữa cạnh và góc trong ∆AHC vuông tại H, chúng ta tính được AH ≈ 2,68cm; HC ≈ 2,25cm
Tương tự trong tam giác vuông HAB, tính được BH ≈ 1,34cm => BC ≈ 3,59cm, S A B C ≈ 4 , 81 c m 2