Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

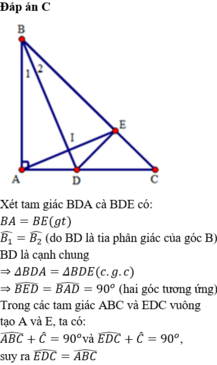
a) Xét tam giác DEB và tam giác DAB có:
EB = BA (gt)
góc EBD = góc DBA (BD là tia phân giác của góc ABC)
DB = BD
=> tam giác DEB = tam giác DAB (c.g.c)
=> AD = AE (2 cạnh tương ứng)
b) Vì tam giác DEB = tam giác DAB (cma)
=> góc CAB = góc DEB = 90 độ
Ta có : góc ECD + góc EDC = 90 độ
góc ABC + góc BCA = 90 độ
=> góc EDC = góc ABC (cùng phụ với góc ACB)
c) Gọi I là giao điểm của BD và AE
Xét tam giác IEB và tam giác IAB có:
BE=BA (gt)
IB chung
góc EBI = góc IBA (BD là p/g của góc ABC)
=> tam giác IEB = tam giác IAB (c.g.c)
=> góc EIB = góc AIB (2 góc tương ứng)
Mà góc EIB + góc AIB = 180 độ
=> góc EIB = góc AIB = 90 độ
=> AE \(\perp\)BD (đpcm)

Bạn tham khảo câu hỏi này nhé :
Câu hỏi của Trần Quốc Tuấn - Toán lớp 7 - Học toán với OnlineMath
Trả lời :
Phạm Thị Thùy Linh tham khảo link nào ??
- Hok tốt !
^_^

a) Áp dụng tính chất tổng ba góc của một tam giác ta có:
A+B+C=1800
Mà A=900(góc vuông)
C=470
=> B=180-90-47=430
ĐS:.................................
#Châu's ngốc

Gọi giao điểm của cạnh BD và AE là F
Xét tam giác BAD và tam giác BED, có:
BA=BE (giả thiết)
Góc DBA=góc BDE (BD là tia pg của gócB)
Cạnh BD chung
=> Tam giác BAD và tam giác BED bằng nhau
Vì tam giác BAD và tam giác BED bằng nhau
=> AF=FE (2 cạnh tương ứng) (1)
Và góc AFB=góc EFB (2 góc tương ứng)
Vì 2 góc AFB và EFB là 2 góc kề bù
=> AFB+EFB=180*
Mà 2 góc AFB và EFB bằng nhau
=> AFB=EFB=180*/2=90*(2)
từ (1),(2) suy ra BD là đường trung trực của AE