Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
GIÚP MÌNH ĐI MÀ!!!!!
\(A=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\left(-\dfrac{5}{\sqrt{3}}\right)^2-4\cdot\dfrac{-\sqrt{2}}{\sqrt{3}}}=\sqrt{\dfrac{25+4\sqrt{6}}{3}}\)
mk đang cần gấp lắm
Theo bài ra :
\(\left(x+5\right)\left(x^2-1\right)\left(3-x\right)>0\)
<=> \(\left(x+5\right)\left(x-1\right)\left(x+1\right)\left(3-x\right)>0\)
Đặt \(\left(x+5\right)\left(x-1\right)\left(x+1\right)\left(3-x\right)=A\)
Ta có bảng xét dấu :
| \(-\infty\) | -5 | -1 | 1 | 3 | \(+\infty\) | ||||
| (x+5) | - | 0 | + | + | + | + | |||
| x2-1 | + | + | 0 | - | 0 | + | + | ||
| 3-x | + | + | + | + | 0 | - | |||
| A | - (loại) | 0 (loại) | +(t.m) | 0(loại) | -(loại) | 0(loại) | +(t.m) | 0(loại) | -(loại) |
Từ bảng xét dấu trên suy ra :
\(A>0\Rightarrow\left[{}\begin{matrix}-5< x< -1\\1< x< 3\end{matrix}\right.\)
a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)
ĐKXĐ:\(x\ge0;y\ge1;z\ge2\)
\(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}=\frac{x+y+z}{2}\)
\(\Leftrightarrow2\sqrt{x}+2\sqrt{y-1}+2\sqrt{z-2}=x+y+z\)
\(\Leftrightarrow\left(x-2\sqrt{x}+1\right)+\left(y-1+2\sqrt{y-1}+1\right)+\left(z-2+2\sqrt{z-2}+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-2\right)^2=0\)
Mà \(\left\{\begin{matrix}\left(\sqrt{x-1}-1\right)^2\ge0\\\left(\sqrt{y-1}-1\right)^2\ge0\\\left(\sqrt{z-2}-2\right)^2\ge0\end{matrix}\right.\)\(\forall x;y;z\)
\(\Rightarrow\left\{\begin{matrix}\left(\sqrt{x-1}-1\right)^2=0\\\left(\sqrt{y-1}-1\right)^2=0\\\left(\sqrt{z-2}-2\right)^2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}\sqrt{x-1}-1=0\\\sqrt{y-1}-1=0\\\sqrt{z-2}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}\sqrt{x-1}=1\\\sqrt{y-1}=1\\\sqrt{z-2}=2\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}x-1=1\\y-1=1\\z-2=4\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}x=2\\y=2\\z=6\end{matrix}\right.\)
=> x02 + y02 + z02 = 22 + 22 + 62 = 44
MONG CÁC ANH CHỊ GIẢI NHANH GIÚP EM
giao điểm (d1) ;và (d2) thỏa he :\(\left\{{}\begin{matrix}2x+my+m+1=0\\\left(m+1\right)x+y+2m=0\end{matrix}\right.\)(I)
\(\Rightarrow\)(I) có nghiệm khi \(m^2+m-2\ne0\Leftrightarrow m\ne1;m\ne-2\)(\(\circledast\))
nghiệm của(I) \(\left\{{}\begin{matrix}x=\dfrac{2m+1}{m+2}=2-\dfrac{3}{m+2}\left(1\right)\\y=\dfrac{m-1}{m+2}=1-\dfrac{3}{m+2}\left(2\right)\end{matrix}\right.\)
lấy về trừ theo về cửa (1) chờ (2) tá dược: x-y = 1
vậy giao điểm của d1 va d2 luôn di động trên đường thẳng : x -y -1 = 0
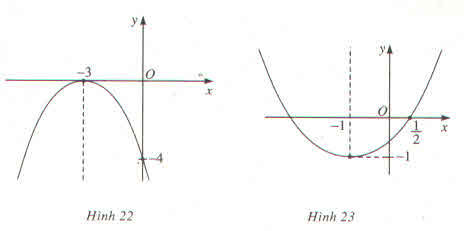
Hình 22
y=ax^2 +bx+c thỏa mãn hệ
\(\left\{{}\begin{matrix}y\left(0\right)=-4\Rightarrow c=-4\\y\left(-3\right)=9a-3b-4=0\\y\left(-6\right)=36a-6b-4=-4\end{matrix}\right.\)
(3) -(2) nhân 2
\(36a-18a-4+8=-4\Rightarrow18a=-8\Rightarrow a=\dfrac{-8}{18}=\dfrac{-4}{9}\)
Thế vào (2) -4-3b-4=0 => b=-8/3
Vậy pa ra bo; cho hình 22 là
\(y=-\dfrac{4}{9}x^2-\dfrac{8}{3}x-4\)
Đáp án: A
Ta tìm phương trình có 2 nghiệm là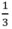
và 1. Ta có thể thử nghiệm vào từng phương trình xem phương trình nào thỏa mãn hoặc giải từng phương trình rồi so sánh nghiệm.
⇒ Chọn đáp án A.