Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

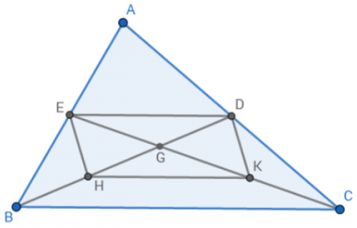
E là trung điểm của AB (CE là đường trung tuyến của tam giác ABC)
D là trung điểm của AC (BD là đường trung tuyến của tam giác ABC)
=> ED là đường trung bình của tam giác ABC.
=> ED // BC (1)
ED = BC/2 (2)
H là trung điểm của GB (gt)
K là trung điểm của GC (gt)
=> HK là đường trung bình của tam giác GBC.
=> HK // BC (3)
HK = BC/2 (4)
Từ (1) và (3)
=> ED // HK (5)
Từ (2) và (4)
=> ED = HK (6)
Từ (5) và (6)
=> DEHK là hình bình hành.
=> G là trung điểm của EK và HD.
=> EG = GK = EK/2
HG = GD = HD/2
CE là đường trung tuyến của tam giác ABC.
=> EG = CE/3
BD là đường trung tuyến của tam giác ABC.
=> DG = BD/3
DEHK là hình chữ nhật
<=> EK = HD
<=> EK/2 = HD/2
<=> EG = DG
<=> CE/3 = BD/3
<=> CE = BD
<=> Tam giác ABC cân tại A
Vậy DEHK là hình chữ nhật khi tam giác ABC cân tại A.
Hình bình hành DEHK có EK _I_ HD
=> DEHK là hình thoi.

a)
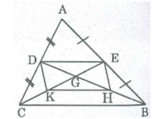
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK
Mà DH = 2/3 BD; EK = 2/3 CE
Nên DH = EK ⇒ BD = CE
⇒ ∆ ABC cân tại A.
Vậy ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.

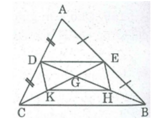
a) Xét \(\Delta ABC\)có:
\(AE=BE\)(giả thiết)
\(AD=CD\)(giả thiết)
\(\Rightarrow DE\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DE//BC\)(tính chất) (1)
Và \(2DE=BC\)(tính chất) (2)
Xét \(\Delta GBC\)có:
\(GH=BH\)(giả thiết)
\(GK=CK\)(giả thiết)
\(\Rightarrow HK\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow HK//BC\)(tính chất) (3)
Và \(2HK=BC\)(tính chất) (4)
Từ (1) và (3)
\(\Rightarrow ED//HK\)(5)
Từ (2) và (4)
\(\Rightarrow2DE=2KH\Rightarrow DE=KH\)(6)
Xét tứ giác DEHK có: (5) và (6).
\(\Rightarrow DEHK\)là hình bình hành (điều phải chứng minh)

Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.




Vì E,H là trung điểm AB,GB nên EH là đtb tg ABG
Do đó EH//AG và \(EH=\dfrac{1}{2}AG\)
Vì F,K là trung điểm CA,CG nên FK là đtb tg AGC
Do đó FK//AG và \(FK=\dfrac{1}{2}AG\)
\(\Rightarrow FK//EH\text{ và }FK=EH\\ \Rightarrow DEHK\text{ là hình bình hành}\)
Để DEHK là hv
\(\Leftrightarrow\left\{{}\begin{matrix}EH\perp HK\\EK\perp HD\end{matrix}\right.\left(1\right)\)
Ta có HK là đtb tg BGC nên HK//BC
Kết hợp \(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}AG\perp BC\left(EH//AG\right)\\BD\perp CE\end{matrix}\right.\)
Mà AG là trung tuyến nên ABC cân tại A
Vậy tam giác ABC cân tại A có trung tuyến BD,CE vuông góc với nhau thì DEHK là hình vuông