Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
Đặt 
suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
Ta có 
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
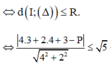
Do đó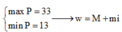 
Đáp án C
HD: Ta có
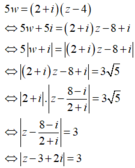
Tập hợp điểm M(z) là đường tròn 
tâm I(3;-2), R=3.
Gọi A(1;2), B(5;2) và E(3;2) là trung điểm của AB suy ra P=MA+MB
Lại có
P lớn nhất 
ME lớn nhất.
Mà 
Vậy 
Mọi điểm M biểu diễn z đều phải thỏa mãn 2 điều kiện: vừa thuộc đường tròn (C) vừa thuộc đường thẳng \(\Delta\) (tham số P)
Do đó, M là giao điểm của (C) và \(\Delta\)
Hay tham số P phải thỏa mãn sao cho (C) và \(\Delta\) có ít nhất 1 điểm chung
Hay hệ pt nói trên có nghiệm (thật ra chi tiết đó là thừa, chỉ cần biện luận (C) và \(\Delta\) có ít nhất 1 điểm chung \(\Rightarrow d\left(I;\Delta\right)\le R\) là đủ)
Đặt \(z=x+yi\Rightarrow w=\dfrac{1}{\sqrt{x^2+y^2}-x-yi}=\dfrac{\sqrt{x^2+y^2}-x+yi}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}=\dfrac{1}{8}\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{2x^2+2y^2-2x\sqrt{x^2+y^2}}=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)}=\dfrac{1}{4}\Rightarrow\dfrac{1}{\sqrt{x^2+y^2}}=\dfrac{1}{4}\)
\(\Rightarrow x^2+y^2=16\)
\(\Rightarrow\) Tập hợp \(z_1;z_2\) là đường tròn tâm O bán kính \(R=4\)
Gọi M, N lần lượt là điểm biểu diễn \(z_1;z_2\), do \(\left|z_1-z_2\right|=2\Rightarrow MN=2\)
Gọi \(P\left(0;5\right)\) và Q là trung điểm MN
\(\Rightarrow P=MP^2-NP^2=\overrightarrow{MP}^2-\overrightarrow{NP}^2=\left(\overrightarrow{MP}-\overrightarrow{NP}\right)\left(\overrightarrow{MP}+\overrightarrow{NP}\right)\)
\(=2\overrightarrow{MN}.\overrightarrow{PQ}=2\overrightarrow{MN}\left(\overrightarrow{PO}+\overrightarrow{OQ}\right)=2\overrightarrow{MN}.\overrightarrow{PO}=2MN.PO.cos\alpha\)
Trong đó \(\alpha\) là góc giữa \(MN;PO\)
Do MN, PO có độ dài cố định \(\Rightarrow P_{max}\) khi \(cos\alpha_{max}\Rightarrow\alpha=0^0\Rightarrow MN||PO\)
Mà MN=2 \(\Rightarrow M\left(\sqrt{15};-1\right);N\left(\sqrt{15};1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PM}=\left(\sqrt{15};-6\right)\\\overrightarrow{PN}=\left(\sqrt{15};-4\right)\end{matrix}\right.\)
\(\Rightarrow P_{max}=PM^2-PN^2=15+36-\left(15+16\right)=20\)
Đáp án C
Đặt 
Số phức z được biểu diễn bởi điểm N(x;y)
Số phức 
được biểu diễn bởi điểm A(-2;1)
Số phức 
được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm
Ta có: |z + 2 - i| + |z - 5 + 6i| = 7
2
Mà AB = 7
2
nên N thuộc đoạn thẳng AB.
Đường thẳng AB: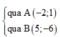 
=> phương trình đường thẳng AB là: x + y + 1 = 0
Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x ∈ [-2;5]
Ta có: 
Xét 
trên [-2;5] ta có: f'(x) = 4(x-1)
Ta có:
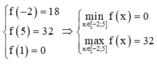
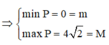
Vậy M + m = 4 2
Đáp án A
Đặt z = x + yi
Có 
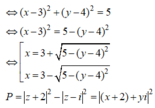
TH1:
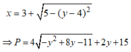
Xét hàm số: 
trên 
Có
Ta có:
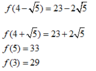
TH2:
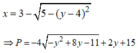
Xét hàm số: 
trên 
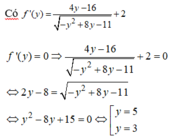
Ta có:
