

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Phương pháp: kết quả:
Tập hợp điểm biểu diễn các số phức z thỏa mãn ![]() với
với ![]() là số phức cho trước,
r
∈
ℝ
là đường tròn I(a,b), bán kính r.
là số phức cho trước,
r
∈
ℝ
là đường tròn I(a,b), bán kính r.

Đặt \(z=a+bi\Rightarrow\overline{z}=a-bi\)
Ta có \(z.\overline{z}=1\Leftrightarrow\left(a+bi\right)\left(a-bi\right)=1\)
\(\Leftrightarrow a^2-b^2i^2=1\Leftrightarrow a^2+b^2=1\)
\(\Rightarrow\) Tập hợp các số phức thỏa mãn điều kiện trên là một đường tròn có tâm là gốc tọa độ, bán kính 1 đơn vị độ dài

Ta có : w - 1 + 2 i = z ⇔ w = z + 1 - 2 i . Suy ra quỹ tích các điểm biểu diễn số phức w có được từ quỹ tích các điểm biểu diễn số phức z bằng cách thực hiện phép tịnh tiến theo v → = ( 1 ; - 2 ) . Do đó quỹ tích quỹ tích các điểm biểu diễn số phức w là đường tròn tâm (-1;1) bán kính bằng 3.
Đáp án D

Đáp án C
Đặt ![]() Số phức w được biểu diễn bởi điểm M (x;y).
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
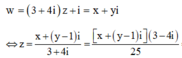
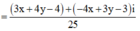
=> |z| = 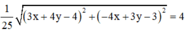
![]()
![]()
![]()
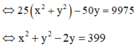
![]()
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: ![]()

Đáp án C.
Ta có:

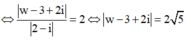
Do đó tập hợp điểm biểu diễn w là đường tròn tâm (3;-2) bán kính R= 2 5