Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp : Sử dụng công thức liên hệ giữa khối lượng và số hạt
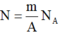
Cách giải :
Năng lượng tỏa ra khi phân hạch hết 1kg Urani
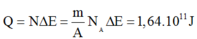

Đáp án A
*Số hạt nhân Urani trong 2g: N = m μ N A = 5 , 1234 . 10 21 .
*Năng lượng tỏa ra khi phân hạch hết 1kg U 92 235 là
Q = N . ∆ E ≈ 1 , 639 . 10 11 ( J )

\(m_t = m_{Na}+ m_H = 22,9837+ 1,0073 = 23,991u.\)
\(m_s = m_{He}+ m_{Ne} = 19,9869+ 4,0015 = 23,9884u.\)
=> \(m_t > m_s\), phản ứng là tỏa năng lượng.
Năng lượng tỏa ra là
\(E = (m_t-m_s)c^2 = 2,6.10^{-3}uc^2 = 2,6.10^{-3}.931,5 = 2,4219 MeV.\)
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCc

Năng lượng liên kết riêng của \(_3^6Li\) là \(W_{lkr1}= \frac{(3.m_p+3.m_n-m_{Li})c^2}{6}=5,2009 MeV.\ \ (1)\)
Năng lượng liên kết riêng của \(_{18}^{40}Ar\) là \(W_{lkr2}= \frac{(18.m_p+22.m_n-m_{Ar})c^2}{40}= 8,6234MeV.\ \ (2)\)
Lấy (2) trừ đi (1) => \(\Delta W = 3,422MeV.\)
Của Ar lớn hơn của Li.

Năng lượng liên kết riêng của hạt nhân
\(W_{lkr}= \frac{W_{lk}}{A} = \frac{(Zm_p+(A-Z)m_n-m_{Be})c^2}{A}\)
\( = \frac{0,0679.931}{10}= 6,3215MeV.\)

Số hạt nhân Heli trong 1 gam Heli là \(N =\frac{m}{A}N_A= \frac{1}{4}6,02.10^{23}= 1,505.10^{23}\)(hạt)
Phương trình phản ứng hạt nhân
\(_1^1p+ _3^7Li \rightarrow _2^4He + _2^4He+ 17,3 MeV\)
Dựa vào phương trình ta thấy để tạo ra 2 hạt nhân Heli thì tỏa ra 17,3 MeV.
Như vậy để tổng hợp 1 gam Heli (chứa 1,505.1023 hạt nhân) thì tỏa ra là
\(\frac{1,505.10^{23}}{2}.17,3 = 13,02.10^{23}MeV\)
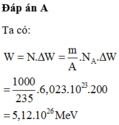

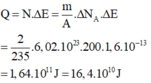
Đáp án A
+ Số hạt nhân Urani trong 1kg:
+ Năng lượng tỏa ra khi phân hạch hết 1kg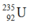 là:
là: