
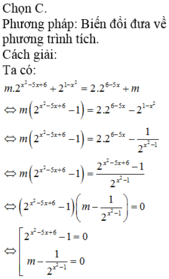

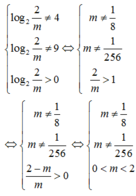
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

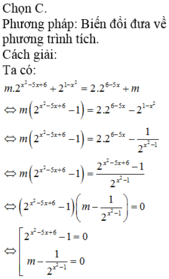

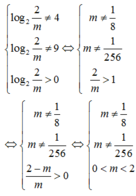

\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)

Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít


\(\Leftrightarrow2^{2x}-1+m.2^x+m\le0\\ \Leftrightarrow\left(2^x-1\right)\left(2^x+1\right)+m\left(2^x+1\right)\le0\\ \Leftrightarrow\left(2^x+1\right)\left(2^x-1+m\right)\le0\)
Vì \(2^x+1>0\forall x\) nên ta có
\(2^x-1+m\le0\Leftrightarrow2^x\le1-m\)
Vẽ đồ thị hàm số \(f\left(x\right)=2^x\),
ta thấy bất phương trình có nghiệm khi và chỉ khi đường thẳng y=1-m nằm trên trục Ox
\(\Rightarrow1-m>0\Leftrightarrow m< 1\) (không có dấu "=")
