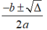Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a.\(\Delta=\left(4m+1\right)^2-8\left(m-4\right)=16m^2+33>0\left(\forall m\in R\right)\)
b.Gia su 2 nghiem cua PT la \(x_1,x_2\left(x_1>x_2\right)\)
Theo de bai ta co;\(x_1-x_2=17\)
Tu cau a ta co:\(x_1=\frac{-4m-1+\sqrt{16m^2+33}}{2}\) \(x_2=\frac{-4m-1-\sqrt{16m^2+33}}{2}\)
\(\Rightarrow\frac{-4m-1+\sqrt{16m^2+33}}{2}-\frac{-4m-1-\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\frac{2\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow16m^2+33=289\)
\(\Leftrightarrow m=4\)
2.
a.\(\Delta'=\left(m-1\right)^2-\left(m+2\right)\left(3-m\right)=2m^2-3m-5=\left(m+1\right)\left(2m-5\right)>0\)
TH1:\(\hept{\begin{cases}m+1>0\\2m-5>0\end{cases}\Leftrightarrow m>\frac{5}{2}}\)
TH2:\(\hept{\begin{cases}m+1< 0\\2m-5< 0\end{cases}\Leftrightarrow m< -1}\)
Xet TH1:\(x_1=\frac{-m+1+\sqrt{2m^2-3m-5}}{m+2}\) \(x_2=\frac{-m+1-\sqrt{2m^2-3m-5}}{m+2}\)
Ta co:\(x^2_1+x^2_2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=x_1+x_2\)
\(\Leftrightarrow\left(\frac{-2m+2}{m+2}\right)^2-\frac{-m^2+5m+6}{\left(m+2\right)^2}=\frac{-2m+2}{m+2}\)
\(\Leftrightarrow\frac{5m^2-13m-2}{\left(m+2\right)^2}=\frac{-2m^2-2m+4}{\left(m+2\right)^2}\)
\(\Rightarrow7m^2-11m-6=0\)
\(\Delta_m=121+168=289>0\)
\(\Rightarrow\hept{\begin{cases}m_1=2\left(l\right)\\m_2=-\frac{3}{7}\left(l\right)\end{cases}}\)
TH2;Tuong tu
Vay khong co gia tri nao cua m de PT co 2 nghiem thoa man \(x^2_1+x^2_2=x_1+x_2\)

Mình nghĩ với pt tổng quát: \(ax^2+bx+c=0\) có \(\Delta=b^2-4ac\)
Nếu như vậy thì: \(1.x^2+6x+m\) có \(\Delta=6^2-4m\)chứ?
Riêng mình thì bài này mình dùng delta phẩy cho lẹ:
Lời giải
Để pt \(x^2+6x+m=0\) có 2 nghiệm phân biệt thì:
\(\Delta'=\left(\frac{b}{2}\right)^2-ac=3^2-m>0\)
\(\Leftrightarrow m< 9\)

a)\(\Delta\)=(m+1)2 -4.1(2m-3) = m2 +2m +1 - 8m +12 =(m2 -6m+9) +4 =(m-3)2 +4 >0 với mọi m
pt luôn có 2 nghiệm pb với mọi m
b) x =3 là nghiệm
32 -(m+1).3 +2m -3 =0
=>-m +3 =0 => m =3

a) phương trình (1) có a=m-1 b'=b/2 = -m-1 c=m
\(\Delta=b'^2-ac=\left(-m-1\right)^2-\left(m-1\right)\cdot m\)
\(=m^2+2m+1-m^2+m=3m+1\)
Phương trình có hai nghiệm <=> \(\Delta\ge0\Leftrightarrow3m+1\ge0\Leftrightarrow m\ge-\frac{1}{3}\)
b) Khi phương trình có hai nghiệm x1, x2, theo hệ thức Vi-ét ta có
\(\hept{\begin{cases}x_1+x_2=\frac{2m+2}{m-1}=2+\frac{4}{m-1}\\x_1\cdot x_2=\frac{m}{m-1}=1+\frac{1}{m-1}\end{cases}}\)
\(\Rightarrow x_1+x_2-4x_1\cdot x_2=-2\)

Câu 1:
Đặt phương trình là (1)
ĐK: \(3x-16y-24\ge0\)
\(3x-16y-24=\sqrt{9x^2+16x+32}\Leftrightarrow\left(3x-16y-24\right)^2=9x^2+16x+32\)
\(\Leftrightarrow9\left(3x-16y-24\right)^2=9\left(9x^2+16x+32\right)\)\(\Leftrightarrow\left(9x-48y-72\right)^2=81x^2+144x+288\)
Với x, y nguyên thì (3y+5) là ước của (-7) và chia cho 3 dư 2
=> (3y+5)=-1 hoặc (3y+5)=-7
+ TH1: \(\left(3y+5\right)=-1\Leftrightarrow y=-2\Rightarrow x=-1\)
+ TH2: \(\left(3y+5\right)=-7\Leftrightarrow y=-4\Rightarrow x=-7\)
Vậy các cặp nghiệm nguyên của (x;y) là: (-1;-2); (-7;-4)
\(\Leftrightarrow\left(9x-48y-72\right)^2=\left(9x+8\right)^2+224\)
\(\Leftrightarrow\left(9x-48y-72\right)^2-\left(9x+8\right)^2=224\)
\(\Leftrightarrow\left(9x-48y-72+9x-8\right)\left(9x-48y-72-9x-8\right)=224\)
\(\Leftrightarrow\left(18x-48y-64\right)\left(-48y-80\right)=224\)
\(\Leftrightarrow-32\left(9x-24y-32\right)\left(3y+5\right)=224\)
\(\Leftrightarrow\left(9x-24y-32\right)\left(3y+5\right)=-7\)
giả sử a là nghiệm chung của 2 phương trình
\(x^2+\text{ax}+bc=0\left(1\right)\) và \(x^2+bx+ca=0\left(2\right)\)
Ta có: \(\hept{\begin{cases}a^2+a\alpha+bc=0\\a^2+b\alpha+ca=0\end{cases}}\)
\(\Rightarrow\alpha\left(a-b\right)+c\left(b-a\right)=0\Rightarrow\left(a-c\right)\left(a-b\right)=0\Rightarrow\alpha=c\ne0\)
Thay \(\alpha=c\)vào (1) ta có: \(c^2+ac+bc=0\Rightarrow c\left(a+b+c\right)=0\Rightarrow a+b+c=0\)
Mặt khác, theo định lý Viet phương trình(1) còn có nghiệm nữa là b, phương trình(2) còn có nghiệm nữa là a. Theo định lý Viet đảo, a và b là hai nghiệm của phương trình \(x^2-\left(a+b\right)x+ab=0\Leftrightarrow x^2+cx+ab=0\left(\text{đ}pcm\right)\)

a. thay m=1 vào pt(1): \(x^2-2.2x+2-4=0\)
<=>\(x^2-4x-2=0\)
\(\Delta'=\left(-2\right)^2-1.\left(-2\right)=4+2=6>0\)
=>\(x_1=-\left(-2\right)+\sqrt{6}=2+\sqrt{6};x_2=2-\sqrt{6}\)
Vậy,,,
b, \(\Delta'=\left[-\left(m+1\right)\right]^2-1.\left(2m-4\right)=m^2+2m+1-2m+4=m^2+5\)
Để pt(1) có 2 nghiệm phân biệt x1,x2 <=>\(\Delta'>0\Leftrightarrow m^2+5>0\) (luôn đúng)
Theo hệ thức vi et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m-4\end{cases}}\)
Theo bài ra ta co;\(\frac{1}{x_1}+\frac{1}{x_2}=2\Leftrightarrow\frac{x_1+x_2}{x_1x_2}=2\Leftrightarrow\frac{2m+2}{2m-4}=2\)
\(\Leftrightarrow2m+2=4m-8\Leftrightarrow2m=10\Leftrightarrow m=5\)

a) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{-35}{1}=-35\\ \Leftrightarrow7x_2=-35\\ \Leftrightarrow x_2=-5\\ x_1+x_2=\dfrac{-m}{1}=-m\\ \Leftrightarrow7+\left(-5\right)=-m\\ \Leftrightarrow-m=2\\ \Leftrightarrow m=-2\)
b) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-\left(-13\right)}{1}=13\\ \Leftrightarrow12,5+x_2=13\\ \Leftrightarrow x_2=0,5\\ x_1x_2=\dfrac{m}{1}=m\\ \Leftrightarrow12,5\cdot0,5=m\\ \Leftrightarrow m=6,25\)
c) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-3}{4}\\ \Leftrightarrow-2+x_2=\dfrac{-3}{4}\\ \Leftrightarrow x_2=\dfrac{5}{4}\\ x_1x_2=\dfrac{-m^2+3m}{4}\\ \Leftrightarrow4x_1x_2=-m^2+3m\\ \Leftrightarrow4\cdot\left(-2\right)\cdot\dfrac{5}{4}+m^2-3m=0\\ \Leftrightarrow m^2-3m-10=0\\ \Leftrightarrow m^2-5m+2m-10=0\\ \Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\\ \Leftrightarrow\left(m+2\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2\\m=5\end{matrix}\right.\)
d) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{5}{3}\\ \Leftrightarrow\dfrac{1}{3}x_2=\dfrac{5}{3}\\ \Leftrightarrow x_2=5\\ x_1+x_2=\dfrac{-\left[-2\left(m-3\right)\right]}{3}=\dfrac{2\left(m-3\right)}{3}=\dfrac{2m-6}{3}\\ \Leftrightarrow3\left(x_1+x_2\right)=2m-6\\ \Leftrightarrow3\left(\dfrac{1}{3}+5\right)=2m-6\\ \Leftrightarrow3\cdot\dfrac{16}{3}+6=2m\\ \Leftrightarrow16+6=2m\\ \Leftrightarrow22=2m\\ \Leftrightarrow m=11\)

Cho phương trình x2 - 2(m - 1)x + m - 3 = 0. a) Chứng minh rằng phương trình luôn có nghiệm với mọi m. b) Gọi x1, x2 là hai nghiệm của phương trình. Tìm giá trị nhỏ nhất của M = (x1)^2 + (x2)^2 - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
Tham khảo bài tương tự tại đó nhé bn !
Mk chưa hok lớp 9 nên ko biết , thông cảm
Có \(x^2-2\left(m-1\right)x-3=0\)
\(\Leftrightarrow x^2-2mx+2x-3=0\)
\(\Leftrightarrow x\left(x-2m+1\right)=3\)
\(\Rightarrow x,x-2m+1\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
| x | 1 | 3 | -1 | -3 |
| x-2m+1 | 3 | 1 | -3 | -1 |
| m | 1/2 | 3/2 | 3/2 | 1/2 |
vậy pt luôn có 2 nghiệm phân biệt.

\(x_o^3=a+\sqrt[3]{a+\sqrt{a^2+b^3}}-\sqrt[3]{a^2+b^3}+a-3\sqrt[3]{\left(a+\sqrt{a^2+b^3}\right)\left(\sqrt{a^2+b^3}-a\right)}.x_o\)
\(\Leftrightarrow x_o^3=2a-3x_o\sqrt[3]{a^2-a^2-b^3}\)
\(\Leftrightarrow x_o^3+2bx_o-2a=0\)
nên x0 là 1 nghiệm của pt đó

Xin phép tách ra để bài giải trở nên đẹp hơn :))
Do X1 ; X2 là 2 nghiệm của phương trình \(5x^2-3x-1\) nên theo định lý Viete ta có:
\(X_1X_2=-\frac{1}{5};X_1+X_2=\frac{3}{5}\) ( 1 )
Khi đó ta có:
\(A=\frac{X_1}{X_2}+\frac{X_1}{X_2+1}+\frac{X_2}{X_1}+\frac{X_2}{X_1+1}-\left(\frac{1}{X_1}+\frac{1}{X_2}\right)\) ( theo mình ở đây là +,không biết có đúng ko :V )
\(=\frac{X_1^2+X_2^2}{X_1X_2}+\frac{X_1^2+X_1+X_2^2+X_2}{X_1X_2+X_1+X_2+1}-\frac{X_2+X_1}{X_1X_2}\)
\(=\frac{\left(X_1+X_2\right)^2-2X_1X_2-\left(X_1+X_2\right)}{X_1X_2}+\frac{\left(X_1+X_2\right)^2-2X_1X_2+\left(X_1+X_2\right)}{\left(X_1+X_2\right)+X_1X_2+1}\)
Bạn thay ( 1 ) vào là ra nhé :)
Đáp án A
Xét phương trình bậc hai một ẩn a x 2 + b x + c = 0 ( a ≠ 0 ) và biệt thức Δ = b 2 - 4 a c
• TH1: Nếu thì phương trình vô nghiệm
• TH2: Nếu thì phương trình có nghiệm kép x 1 = x 2 =
• TH3: Nếu thì phương trình có hai nghiệm phân biệt x 1 , 2 =