Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Ghi nhớ:
-Phép thử “gieo hai đồng tiền phân biệt” thì hai kết quả SN, NS của phép thử là khác nhau.
-Phép thử “gieo n đồng xu phân biệt” thì không gian mẫu có 2 n phần tử, với n ∈ ℕ * .

Nếu không quan tâm thứ tự của sấp và ngửa thì đáp án là A
Có quan tâm thứ tự thì đáp án là B
Hơi khó nghĩ, nghiêng về B hơn

Đặt \(f\left(x\right)=\left(2m^2-5m+2\right)\left(x+2\right)^{2019}\left(x^{2020}-4\right)+5x-1\)
Do \(f\left(x\right)\) là hàm đa thức nên liên tục và xác định trên R
Ta có: \(f\left(-2\right)=-11< 0\)
Lại có: \(4>1\Rightarrow\sqrt[2020]{4}>1\Rightarrow5\sqrt[2020]{4}>1\)
\(\Rightarrow f\left(\sqrt[2020]{4}\right)=5\sqrt[2020]{4}-1>0\)
\(\Rightarrow f\left(-2\right).f\left(\sqrt[2020]{4}\right)< 0;\forall m\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;\sqrt[2020]{4}\right)\) hay pt đã cho luôn luôn có nghiệm với mọi m

Không gian mẫu \(\Omega=\left\{S;N;1;2;3;4;5;6\right\}\)
\(\Rightarrow n\left(\Omega\right)=8\)
\(A=\left\{S;2;4;6\right\}\)
\(\Rightarrow n\left(A\right)=4\)
Xác suất của biến cố \(A\) :
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{8}=\dfrac{1}{2}\)

Theo BĐT Cauchy: \(\left\{{}\begin{matrix}\sqrt{ab}\le\dfrac{a}{4}+b\\\sqrt[3]{abc}\le\dfrac{1}{3}\left(\dfrac{a}{4}+b+4c\right)\end{matrix}\right.\)
\(\Rightarrow a+\sqrt{ab}+\sqrt[3]{abc}\le a+\dfrac{a}{4}+b+\dfrac{1}{3}\left(\dfrac{a}{4}+b+4c\right)=\dfrac{4}{3}\left(a+b+c\right)\)
\(\Rightarrow P\ge\dfrac{1346}{\dfrac{4}{3}\left(a+b+c\right)}-\dfrac{2019}{\sqrt{a+b+c}}=\dfrac{2019}{2\left(a+b+c\right)}-\dfrac{2019}{\sqrt{a+b+c}}\)
\(\Rightarrow\dfrac{2P}{2019}\ge\dfrac{1}{a+b+c}-\dfrac{2}{\sqrt{a+b+c}}=\left(\dfrac{1}{\sqrt{a+b+c}}\right)^2-2.\dfrac{1}{\sqrt{a+b+c}}+1-1\)
\(\Rightarrow\dfrac{2P}{2019}\ge\left(\dfrac{1}{\sqrt{a+b+c}}-1\right)^2-1\ge-1\)
\(\Rightarrow P\ge\dfrac{-2019}{2}\)
\(\Rightarrow P_{min}=\dfrac{-2019}{2}\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\dfrac{a}{4}=b=4c\\\dfrac{1}{\sqrt{a+b+c}}-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{16}{21}\\b=\dfrac{4}{21}\\c=\dfrac{1}{21}\end{matrix}\right.\)

1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64

Chọn C
Ta có: ∑ k = 0 2020 C 2020 k - ∑ k = 0 2019 C 2019 k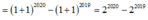
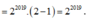
Vì một đồng xu có hai mặt nên khi gieo 2019 đồng xu phân biệt ta có 2 2019 kết quả có thể xảy ra của phép thử. Vậy số
phần tử của không gian mẫu là n( Ω ) = 2 2019 .