Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 5x + 10 = 5(x + 2)
25x2 + 50x = 25x(x + 2)
⇒ Nhân tử chung của chúng là: 5(x + 2)
b)
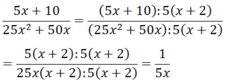

Chứng minh tử thức (hoặc mẫu thức) chia hết cho 11 thì mẫu thức (hoặc tử thức) chia hết cho 11 nghĩa là ta chứng minh nếu \(k^2-5k+8\)chia hết cho 11 thì \(k^2+6k+9\)cũng chia hết cho 11 và ngược lại.
Ta có :
\(k^2-5k+8\)chia hết cho 11
Mà \(11k\)chia hết cho 11
\(11\)chia hết cho 11
\(\Rightarrow k^2-5k+8+11k+11\)chia hết cho 11
\(\Rightarrow k^2+6k+19\)chia hết cho 11
Chứng minh ngược lại :
\(k^2+6k+19\)chia hết cho 11
Mà \(11k;11\)chia hết cho 11
\(\Rightarrow k^2+6k+19-11k-11\)chia hết cho 11
\(\Rightarrow k^2-5k+8\)chia hết cho 11
Vậy ...

a)\(\dfrac{3x^2-12x+12}{x^4-8x}=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x^3-2^3\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

Gọi tử số phân số cần tìm là \(a\)
Gọi mẫu số phân số cần tìm là \(a+5\)
Nếu tăng tử số thêm 5 đơn vị ta được \(a+5\)
Nếu tăng mẫu số thêm 5 đơn vị ta được \(a+5+5=a+10\)
Ta có Nếu tăng cả tử và mẫu của nó thêm 5 đơn vị thì được phân số mới bằng phân số \(\frac{2}{3}\) .Tìm phân số ban đầu
\(\Rightarrow\frac{a+5}{a+10}=\frac{2}{3}\)
\(\Rightarrow\frac{3\left(a+5\right)}{3\left(a+10\right)}=\frac{2\left(a+10\right)}{3\left(a+10\right)}\)
\(\Rightarrow\frac{3a+15}{3\left(a+10\right)}=\frac{2a+20}{3\left(a+10\right)}\)
\(\Rightarrow3a+15=2a+20\)
\(\Rightarrow3a-2a=20-15\)
\(\Rightarrow a=5\)
Vậy tử số là 5
mẫu số là 5 + 5 = 10
=> Phân số cần tìm là \(\frac{5}{10}\)
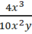
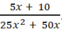
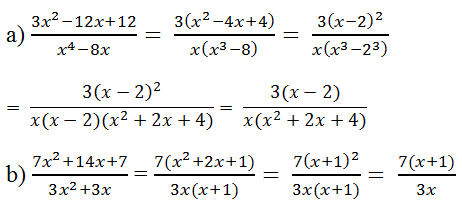
a) Nhân tử chung của cả tử và mẫu: 2x2
b)