Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

nói lại em kém anh 7 năm nhé. Nên bọn em cần gợi ý mới làm được chứ. Với lại hình như anh học cái này thì phải bít chứ. Its ra cũng phải có gợi ý...!

Chọn gốc toạ độ tại VTCB; chiều dương hướng xuống dưới.
Độ giãn của hệ lò xo + dây đàn hồi khi vật ở VTCB:
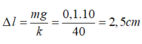
- Khoảng thời gian từ khi thả vật đến khi vật đạt độ cao cực đại lần thứ nhất được chia làm hai giai đoạn:
+ Giai đoạn 1 (sợi dây bị kéo giãn tương đương như một lò xo): Vật đi từ vị trí biên x = 5cm đến vị trí x = -∆l = -2,5cm
+ Giai đoạn 2 (khi dây bị trùng lực đàn hồi bị triệt tiêu): Vật đi từ vị trị x = -∆l = -2,5cm đến biên âm.
- Giai đoạn 1:
Hệ dao động gồm lò xo và sợi dây đàn hồi nhẹ có cùng chiều dài tự nhiên treo thẳng đứng vào cùng một điểm cố định đầu còn lại của lò xo và sợi dây gắn vào vật nặng được coi như hai lò xo mắc song song
=> Độ cứng của hệ: k = k1 + k2 = 10 + 30 = 40 N/m
Chu kì dao động của hệ:
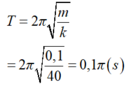
Ban đầu vật ở VTCB, kéo vật thẳng đứng xuống dưới một đoạn a = 5cm rồi thả nhẹ => A = 5cm.
Thời gian vật đi từ x = 5cm đến x = -2,5cm được biểu diễn trên đường tròn lượng giác:
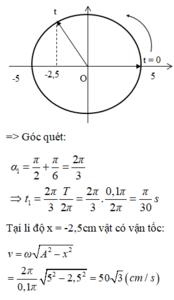
- Giai đoạn 2:
Độ giãn của lò xo ở VTCB: ∆ l ' = m g k 1 = 10 c m => tại vị trí lò xo không biến dạng x = -10cm
Vật dao động điều hoà với chu kì và biên độ:
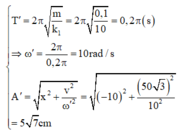
Vật đi từ vị trí x = -∆l = -10cm đến biên âm x = - 5 7 c m được biểu diễn trên đường tròn lượng giác:
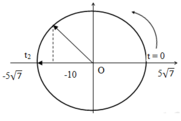
Từ đường tròn lượng giác ta tính được:
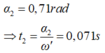
=> Khoảng thời gian kể từ khi thả vật đến khi vật đạt độ cao cực đại: t = t1 + t2 = 0,175s
Đáp án C

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
Độ biến dạng tại vị trí cân bằng của dây là
Chia dao động của vật làm 3 giai đoạn được biểu diễn như hình vẽ
Đáp án B