Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là C n 2 , trong đó có n cạnh, suy ra số đường chéo là C n 2 - n
+ Đa giác đã cho có 135 đường chéo nên C n 2 − n = 135
+ Giải phương trình
n ! n − 2 ! 2 ! = 135 , n ∈ ℕ , n ≥ 2 ⇔ n − 1 n − 2 n = 270 ⇔ n 2 − 3 n − 270 = 0 ⇔ n = 18 n h a n n = − 15 l o a i ⇔ n = 18
Lấy 3 còn lại 9 => nó là tg đều khi 2 đỉnh của tg phải cách nhau qua 3 đỉnh khác
Chia đỉnh đa giác thành 3 nhóm, mỗi nhóm có 4 đỉnh kề nhau, khi lấy 1 đỉnh ở nhóm này làm 1 đỉnh tg thì 2 đỉnh kia sẽ nằm tg ứng trong 2 nhóm còn lại, và số cách lấy 1 đỉnh trong 1 nhóm để làm đỉnh đa giác là 4 => có 4 tg đều có thể lập đc
=> Xác suất = ......
Nếu đã hiểu bài này, b có thể đưa ra 1 công thức: đó là nếu đa giác đều có 3n đỉnh (n thuộc N) thì số tam giác đều như trên là n
Chú ý chỉ là quan tâm đến chữ "đều" mà thôi, từ đó suy ra đc những tính chất mà đề yêu cầu, VD trong bài này, tính chất là mỗi đỉnh của tg đều pải cách nhau qua 3 đỉnh khác của đa giác, từ đó mới suy ra cách chọn ntn.
Còn công thức b co thể xem trên GL về tổ hợp xác suất trong hình học.
Một số khi chia cho 4 có 4 khả năng: chia hết (có dạng 4k), dư 1 (có dạng 4k + 1), dư 2 (có dạng 4k + 2), dư 3 (có dạng 4k + 3 = 4(k+1) - 1 = 4n - 1, với n = k+1).
Vì số nguyên tố lớn hơn 2 nên số đó không chia hết cho 2 => số đó không chia hết cho 2 và cho 4. Vậy nó chỉ có dạng 4k + 1 hoặc 4n - 1
vì 3n^2 chia hết cho 3 nên để A chia hết cho 3 thì ta CM
n^3+2n=n*(n*n+2) vì n là số nguyên nên n có dạng 3k; 3k+1;3k+2(k thuộc Z)
nếu n=3k thì n*(n*n+2) luôn luôn chia hết cho 3
nếu n=3k+1 thì n*n=(3k+1)*(3k+1)=9k^2+3k+3k+1 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
nếu n=3k+2 thì n*n=(3k+2)*(3k+2)=9k^2+6k+6k+4 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
vậy biểu thức trên luôn luôn chia hết cho 3 với mọi n thuộcZ
câu b)để A chia hết cho 15 thì n^3+3n^2+2n phải chia hết cho 3;5(vì ƯCLN(3;5)=1)
Mà theo câu a thì A luôn luôn chia hết cho 3 với n thuộc Z
nên ta chỉ cần tìm giá trị của n để A chia hết cho5
để A chia hết cho 5 thì n^3 phải chia hết cho 5;3n^2 phải chia hết cho 5;2n phải chia hết cho 5
nên n phải chia hết cho 5(vì ƯCLN(3;5)=1;ƯCLN(2;5)=1 nên n^3;n^2;n phải chia hết cho 5 nên ta suy ra n phải chia hết cho 5)
mà 1<n<10 nên n=5(n là số nguyên dương)
vậy giá trị của n thỏa mãn đề bài là 5
Đáp án A
Phương pháp
Tìm số cạnh và số đường chéo của đa giác đều n cạnh.
Cách giải
Khi nối hai đỉnh bất kì của đa giác ta được một số đoạn thẳng, trong đó bao gồm cạnh của đa giác và đường chéo của đa giác đó.
Đa giác đều n cạnh có n đỉnh, do đó số đường chéo là C n 2 − n
Theo giả thiết bài toán ta có
C n 2 − n = n ⇔ C n 2 = 2 n ⇔ n ! 2 ! n − 2 ! = 2 n ⇔ n n − 1 = 4 n ⇔ n − 1 = 4 ⇔ n = 5
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
Đáp án C
Phương pháp: Số tam giác vuông bằng số đường kính của đường tròn có đầu mút là 2 đỉnh của đa giác (H) nhân với (2n – 2) tức là số đỉnh còn lại của đa giác.
Cách giải: Số phần tử của không gian mẫu: n Ω = C 2 n 3
Tam giác vuông được chọn là tam giác chứa một cạnh là đường kính của đường tròn tâm O.
Đa giác đều 2n đỉnh chứa 2n đường chéo là đường kính của đường tròn tâm O, mỗi đường kính tạo nên 2n – 2 tam giác vuông.
Do đó số tam giác vuông trong tập S là: 
Xác suất chọn một tam giác vuông trong tập S :
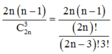
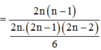
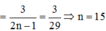
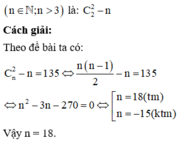
Chọn C
Với hai đỉnh sẽ cho ta một đoạn thẳng, do đó số đoạn thẳng được tạo ra từ n đỉnh là C n 2
Đa giác có n đỉnh sẽ có n cạnh. Trong số C n 2 đoạn thẳng có n đoạn thẳng là cạnh của đa giác. Do đó số đường chéo của đa giác là