Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

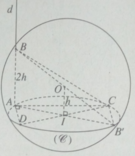
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)

Đáp án là A
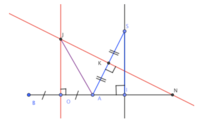
* Gọi J là tâm mặt cầu qua đường tròn tâm O và điểm S => J nằm trên đường trung trực của AB và SA
*Tam giác SIA vuông tại I.
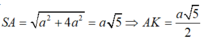
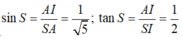
*Ta có: Góc N và S bằng nhau vì cùng phụ với góc S A N ^
* Tam giác AKN vuông tại K
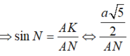
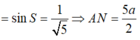
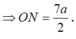
* Tam giác OJN vuông tại O
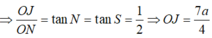
* Tam giác AOJ vuông tại O
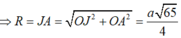
Cách 2
Gắn hệ trục toạ độ Oxy sao cho A, B, O thuộc tia Ox, S thuộc tia Oy và giả sử a = 1.
Khi đó A(1;0), B(3;0), S(0;2)
![]()
là đường tròn tâm J qua 3 điểm A, S, B
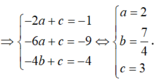
Suy ra:
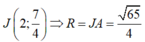
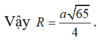

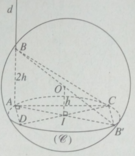
Diện tích tam giác BCD bằng:
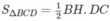
Diện tích này lớn nhất khi AI // CD.

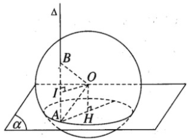
Mặt phẳng (ABO) qua tâm O của hình cầu nên cắt mặt cầu theo đường tròn lớn qua A và B. Gọi I là trung điểm của đoạn AB ta có OI ⊥ AB. Vì AB // OH nên AIOH là hình chữ nhật.
Do đó
![]()
Vậy AB = 2AI = r
Chú ý: Có thể nhận xét rằng tam giác OAB cân tại O (OA = OB) và có góc ∠ OAB = 60 ° nên OAB là tam giác đều và suy ra AB = OA = OB = r.

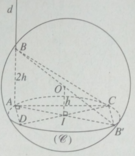
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

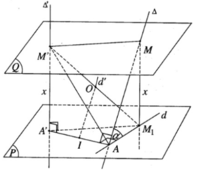
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.

- Nếu H nằm ở nửa dưới đoạn SO thì \(R\ge\dfrac{SO}{2}=\dfrac{3}{2}\)
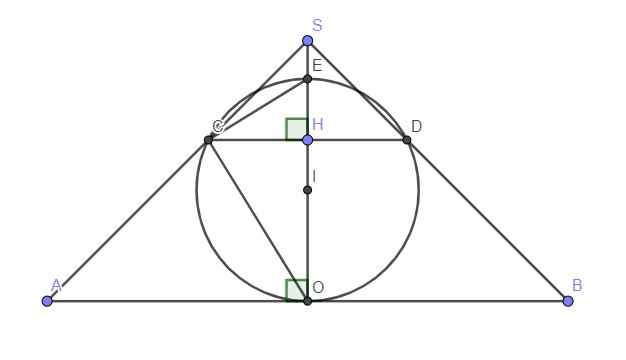
- Nếu H nằm ở nửa trên đoạn SO, thực hiện mặt cắt qua trục nón như hình vẽ
\(SO=OA=3\Rightarrow SOA\) vuông cân \(\Rightarrow SCH\) vuông cân
\(\Rightarrow CH=SH=3-OH=3-\left(R+IH\right)=3-R-\sqrt{R^2-CH^2}\)
\(\Rightarrow3-R=CH+\sqrt{R^2-CH^2}\le\sqrt{2\left(CH^2+R^2-CH^2\right)}=R\sqrt{2}\)
\(\Rightarrow R\left(\sqrt{2}+1\right)\ge3\Rightarrow R\ge\dfrac{3}{\sqrt{2}+1}=3\left(\sqrt{2}-1\right)\)
\(V_{min}=\dfrac{4}{3}\pi R_{min}^3=8,037\)
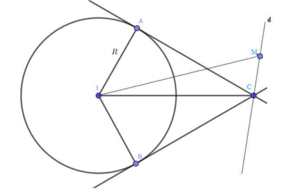
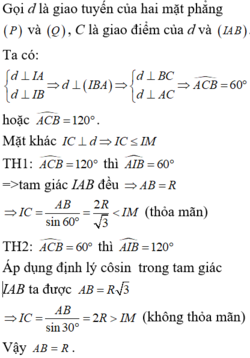

* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:
AM = AI ( tính chất hai tiếp tuyến cắt nhau)
* Tương tự có BM = BI.
* Xét hai tam giác AMB và tam giác AIB có:
AM = AI
BM = BI
AB chung
Suy ra: ∆ AMB = ∆ AIB ( c.c.c)