Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi f=f2=100Hz, công suất toàn mạch cực đại \(\Rightarrow \omega_2=\dfrac{1}{\sqrt{LC}}\)
\(\cos\varphi_1=\dfrac{R+r}{\sqrt{(R+r)^2+Z_L^2}}=0,6\)(1)
\(\cos\varphi_2=\dfrac{R+r}{\sqrt{(R+r)^2+(Z_L-Z_C)^2}}=0,8\)(2)
Đặt \(X=R+r\)
\((1)\Rightarrow X^2=0,36X^2+0,36Z_L^2\Rightarrow 0,64X^2=0,36Z_L^2\)(3)
\((2)\Rightarrow X^2=0,64X^2+0,64(Z_L-Z_C)^2\Rightarrow 0,36X^2=0,64(Z_L-Z_C)^2\)(4)
Từ (3) và (4) \(\Rightarrow\dfrac{0,36}{0,64}Z_L^2=\dfrac{0,64}{0,36}(Z_L-Z_C)^2\)
\(\Rightarrow \dfrac{0,36}{0,64}Z_L=|Z_L-Z_C|\)
TH1: \(\Rightarrow \dfrac{0,36}{0,64}Z_L=Z_L-Z_C\)\(\Rightarrow \dfrac{0,28}{0,64}Z_L=Z_C\)\(\Rightarrow \dfrac{0,28}{0,64}\omega_1 L=\dfrac{1}{\omega_1C}\)\(\Rightarrow \omega_1=\sqrt{\dfrac{0,64}{0,28}}.\omega_2\)
\(\Rightarrow f_1=\sqrt{\dfrac{0,64}{0,28}}.f_2=...\)
Bạn làm tiếp với TH2 nhé :)

Đáp án D
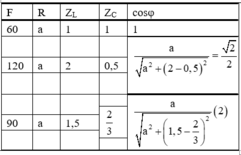
Dùng phương pháp chuẩn hóa:
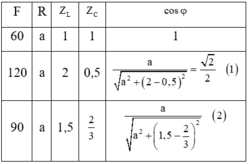
Giải (1) ta được: 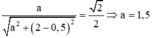 Thay a=1,5 vào (2) ta có:
Thay a=1,5 vào (2) ta có:
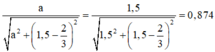

Đáp án D
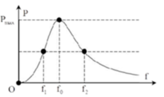
+ f 1 và f 2 là hai giá trị của tần số cho cùng công suất tiêu thụ trên mạch
![]()
là giá trị của tần số để công suất tiêu thụ trên mạch là cực đại (mạch xảy ra cộng hưởng).
=> P 3 > P 4

Đáp án D
Ta có, giá trị của tần số để công suất tiêu thụ của mạch đạt cực đại là: f 0 = f 1 f 2 = 49.64 = 56 H z
Nhận thấy: f 0 = f 3 = 56 H z , thì công suất tiêu thụ của mạch đạt cực đại P max = P 3 , vậy khi f 4 = 60 H z thì công suất tiêu thụ của mạch là P 4 và P 4 < P max = P 3
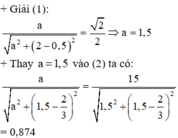

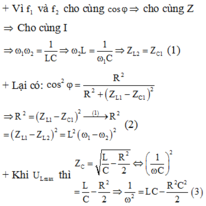
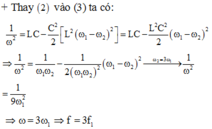


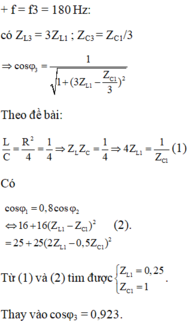
Đáp án A
+ Hệ thức liên hệ f 1 f 2 = f 3 2