
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

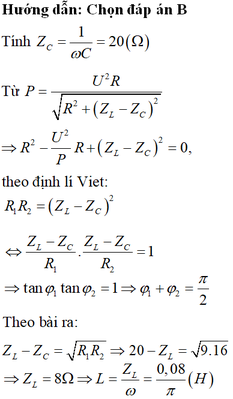

\(Z_L=100\Omega\)
\(Z_C=40\Omega\)
Theo giả thiết ta có:
\(R_1.R_2=(Z_L-Z_C)^2=60^2\)
\(R_1+R_2=\dfrac{U^2}{P}\)
\(\tan\varphi_1=\dfrac{60}{R_1}\)
\(\tan\varphi_2=\dfrac{60}{R_2}\)
Có: \(\varphi_1=2.\varphi_2\Rightarrow \tan \varphi_1=\tan 2\varphi_2=\dfrac{2\tan\varphi_2}{1-\tan^2\varphi_2}=\dfrac{60}{R_1}\)
\(\Rightarrow \dfrac{2\dfrac{60}{R_2}}{1-(\dfrac{60}{R_2})^2}=\dfrac{60}{R_1}\)
Biến đổi ta tìm đc \(R_2=60\sqrt 3\); \(R_1=20\sqrt 3\)
\(\Rightarrow P=\dfrac{U^2}{R_1+R_2}=60\sqrt 3(W)\)

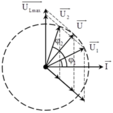
Ta biễu diễn trên giãn đồ vecto. Hai giá trị của L cho cùng một điện áp hiệu dụng trên cuộn cảm → U 1 → và U 2 → đối xứng với ứng với U L m a x
→ Ta có φ 1 + φ 2 = 2 φ 0 → φ 0 = 0 , 785 rad.
Đáp án C

Chọn đáp án D
Từ đồ thị biểu diễn sự phụ thuộc của φ theo L ta có: tại L = 0,2 H thì φ = 30 0
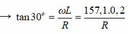
![]()