Cho m > n, chứng minh: a) m + 2017 > n + 2016 b) n - 1 < m + 2

Cho m > n, chứng minh:a) m + 2017 > n + 2016 b) n

TD

Tranh Diệp Phi

25 tháng 6 2020

1.Giải phương trình sau: [x-2015] + [2x-2016]= x-2017 2. Cho ba số thực a,b,c khác nhau thỏa mãn: $a+\frac{2020}{b}=b+\frac{2020}{c}=c+\frac{2020}{a}$. Chứng minh rằng $a^2+b^2+c^2=2020^3$ 3. Cho a,b,c là số dương thỏa mãn a+b+c=9. Chứng minh: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge1$ 4. Chứng minh bất đẳng thức sau vớ a,b,c là các số dương: $\left(a+b+c\right)\times\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9$ 5. Cho a >0, b >0, c...

Đọc tiếp

#Toán lớp 8

0

TK

Thị Kim Vĩnh Bùi

16 tháng 12 2019

CHO a,b,c

∈N∈N thỏa mãn ƯCLN(a,b,c)=1 và c=$\frac{ab}{a-b}$.Chứng minh a-b là số nguyên tố

#Toán lớp 8

0

AD

Ánh Dương

31 tháng 3 2019

1. Cho các số tự nhiên a, b, c thỏa mãn $a^2+b^2+c^2=ab+bc+ca$và a+b+c=3. Tính $M=a^{2016}+2015b^{2015}+2020c$

2. cho x>Y>0. Chứng minh $\frac{x-y}{x+y}< \frac{x^2-y^2}{x^2+y^2}$

#Toán lớp 8

2

AH

Akai Haruma

Giáo viên

31 tháng 3 2019

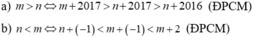
Bài 1:

Ta có:

$a^2+b^2+c^2=ab+bc+ac$

$\Leftrightarrow a^2+b^2+c^2-ab-bc-ac=0$

$\Leftrightarrow 2a^2+2b^2+2c^2-2ab-2bc-2ac=0$

$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$

Vì $(a-b)^2, (b-c)^2, (c-a)^2\geq 0, \forall a,b,c\in\mathbb{R}$. Do đó để tổng của chúng bằng $0$ thì $(a-b)^2=(b-c)^2=(c-a)^2=0\Rightarrow a=b=c$.

Kết hợp với $a+b+c=3$ suy ra $a=b=c=1$

Do đó:

$M=a^{2016}+2015b^{2015}+2020c=1+2015+2020=4036$

Đúng(0)

AH

Akai Haruma

Giáo viên

31 tháng 3 2019

Bài 2:

Xét hiệu:

$\frac{x-y}{x+y}-\frac{x^2-y^2}{x^2+y^2}=(x-y)\left(\frac{1}{x+y}-\frac{x+y}{x^2+y^2}\right)$

$=(x-y).\frac{x^2+y^2-(x+y)^2}{(x+y)(x^2+y^2)}=\frac{(x-y)(x^2+y^2-x^2-2xy-y^2)}{(x^2+y^2)(x+y)}$

$=\frac{-2xy(x-y)}{(x^2+y^2)(x+y)}$

Vì $x>y>0\Rightarrow -2xy(x-y)< 0; (x^2+y^2)(x+y)>0$

$\Rightarrow \frac{x-y}{x+y}-\frac{x^2-y^2}{x^2+y^2}=\frac{-2xy(x-y)}{(x^2+y^2)(x+y)}< 0$

$\Rightarrow \frac{x-y}{x+y}< \frac{x^2-y^2}{x^2+y^2}$

Ta có đpcm.

Đúng(0)

JM

Jang Min

4 tháng 12 2018

1/ Tìm dư trong phép chia $\left(14^8\right)^{2004}$ cho 11.

2/ Tìm số NN có 14 chữ số, biết rằng NN chia 7741 dư 2017, chia 2017 dư 2013, chia 2013 dư 2011.

3/ Tìm dư khi chia $A=1^{2015}+2^{2015}+3^{2015}+...2015^{2015}$ cho 11.

#Toán lớp 8

0

LT

Law Trafargal

27 tháng 11 2019

Cho biểu thức A = −x^2−2x−2

b, Chứng minh rằng khi A xác định thì A luôn nhận giá trị âm

c,Tìm GTLN của A

d, Tìm x nguyên để A nhận giá trị nguyên

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 11 2019

b)Ta có: $A=-x^2-2x-2$

$=-\left(x^2+2x+2\right)=-\left(x+1\right)^2-1$

Ta có: $\left(x+1\right)^2\ge0\forall x$

$\Rightarrow-\left(x+1\right)^2\le0\forall x$

$\Rightarrow-\left(x+1\right)^2-1\le-1\forall x$

Vì -1 là số âm nên khi giá trị của biểu thức A được xác định thì biểu thức A luôn nhận giá trị âm

c)

Ta có: $A=-x^2-2x-2$

$=-\left(x^2+2x+2\right)=-\left(x+1\right)^2-1$

Ta có: $\left(x+1\right)^2\ge0\forall x$

$\Rightarrow-\left(x+1\right)^2\le0\forall x$

$\Rightarrow-\left(x+1\right)^2-1\le-1\forall x$

Dấu '=' xảy ra khi

$-\left(x+1\right)^2=0\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x+1=0\Leftrightarrow x=-1$

Vậy: GTLN của đa thức $A=-x^2-2x-2$ là -1 khi và chỉ khi x=-1

Đúng(0)

SG

Sách Giáo Khoa

5 tháng 5 2017

Cho $m< n$, chứng tỏ :

a) $2m+1< 2n+1$

b) $4\left(m-2\right)< 4\left(n-2\right)$

c) $3-6m>3-6n$

#Toán lớp 8

1

NT

Nguyen Thuy Hoa

4 tháng 7 2017

Bất phương trình bậc nhất một ẩn

Đúng(0)

US

Uchiha Sasuke

19 tháng 4 2019 - olm

Bài 1:

a)Cho a và b là các số dương,chứng tỏ:$\frac{a}{b}$+$\frac{b}{a}$ $\ge2$

b)Với số a bất kì,chứng tỏ:a(a+2)<(a+1)²

c)Cho m>0,n>0,chứng tỏ:(m+n)($\frac{1}{m}$ +$\frac{1}{n}$ )$\ge4$

Giải giúp mình nha!

Thanks trước

Ai giải đc mk tick

#Toán lớp 8

6

GL

ღ๖ۣۜLinh's ๖ۣۜLinh'sღ] ★we are one★

19 tháng 4 2019

a, Áp dụng bđt Cauchy ta có

$\frac{a}{b}+\frac{b}{a}\ge2\sqrt{\frac{a}{b}.\frac{b}{a}}=2$

Đúng(0)

GL

ღ๖ۣۜLinh's ๖ۣۜLinh'sღ] ★we are one★

19 tháng 4 2019

b, a(a+2)<(a+1)²

=>a²+2a<a²+2a+1(đúng)

Đúng(0)

HT

Hoàng Thị Mai Trang

27 tháng 2 2020

Bài 1: a) Cho x>0,y>0 và m,n là hai số thực .Chứng minh rằng $\frac{m^2}{x}+\frac{n^2}{y}$ ≥ $\frac{\left(m+n\right)^2}{x+y}$

b)Cho a,b,c là 3 số dương thỏa mãn abc=1.Chứng minh rằng : $\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}$ ≥$\frac{3}{2}$

#Toán lớp 8

2

NV

Nguyễn Việt Lâm

Giáo viên

27 tháng 2 2020

a/ Bạn cứ khai triển biến đổi tương đương thôi (mà làm biếng lắm)

b/ Đặt $\left(a;b;c\right)=\left(\frac{1}{x};\frac{1}{y};\frac{1}{z}\right)\Rightarrow xyz=1$

$VT=\frac{x^3yz}{y+z}+\frac{y^3zx}{z+x}+\frac{xyz^3}{x+y}=\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}$

$VT\ge\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{1}{2}\left(x+y+z\right)\ge\frac{1}{2}.3\sqrt[3]{xyz}=\frac{3}{2}$

Dấu "=" xảy ra khi $x=y=z=1$ hay $a=b=c=1$

Đúng(0)

HT

Hoàng Thị Mai Trang

27 tháng 2 2020

cảm ơn bạn nhưng nạ có thể giải nốt cậu a hộ mình đc ko

Đúng(0)

SG

Sách Giáo Khoa

5 tháng 5 2017

Cho $m>n$, chứng tỏ :

a) $m+3>n+1$

b) $3m+2>3n$

#Toán lớp 8

1

NT

Nguyen Thuy Hoa

4 tháng 7 2017

Bất phương trình bậc nhất một ẩn

Đúng(0)

DH

Deo Ha

13 tháng 5 2017

Cho 2 số a và b thỏa mãn a≥; b≥1. Chứng minh: $\dfrac{1}{1+a^2}+\dfrac{1}{1+b^2}\ge\dfrac{2}{1+ab}$

#Toán lớp 8

2

Q

qwerty

13 tháng 5 2017

1/(1+a^2) +1/(1 +b^2) >= 2/(1+ ab)

<=>1/ (1+a^2) +1/(1 +b^2) - 2/(1+ ab) >=0

<=> [1/(1+a^2) - 1/(1+ ab)] + [1/(1 +b^2) - 1/(1+ ab) ] >= 0

<=> [ a(b-a)/(1+a^2)(1+ ab) ] + [ b(a-b)/(1 +b^2)(1+ ab)] >=0

<=> [ a(b-a)(1 +b^2) - b(b-a)(1+a^2) ]/[(1+a^2)(1 +b^2)(1+ ab)^2]>= 0

<=> [(b-a)(a + ab^2 - b + ba^2) ]/[(1+a^2)(1 +b^2)(1+ ab)^2]>= 0

<=> [(b-a)[(a- b)+ ab(b-a)] ]/[(1+a^2)(1 +b^2)(1+ ab)^2]>= 0

<=> [(b-a)^2(ab-1]/[(1+a^2)(1 +b^2)(1+ ab)^2]>= 0

Mẫu số luôn lớn hơn 1

[(b-a)^2 >= 0 với mọi a, b

Vì a, b >= 1 nên ( ab - 1 ) >= 0

=> đpcm.

Đúng(0)

B

BW_P&A

13 tháng 5 2017

Ôn tập: Phân thức đại số

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP