Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

a d e m n b c i h
a, tam giác ade cân a
=> góc d = góc e và ad = ae
tam giác adb = tam giác aec ( cgc)
=> ab=ac
=> tam giác abc cân a
b, tam giác bmd vuông m và tam giác cne vuông n
góc m = góc n =90 độ
góc d = góc e
bd = ce
=> bmd = cne (ch-gn)
=> bm = cn
c, có tam giác bmd = tam giác cne
=> góc mbd = góc nce
mà góc cbi đối đỉnh góc mbd, bci đối đỉnh nce
=> góc cbi = góc bci
=> tam giác ibc cân i
d, lây h là trung điểm bc
tam giác abc cân a có ah là đường trung tuyến úng với bc
=> ah vừa là trung tuyến vừa là đường cao ứng với bc
cmtt với ibc => ih vừa là trung tuyến vừa là đường cao ứng với bc
=> a,i,h thẳng hàng
=> ai vừa trung tuyến vừa là đường cao tam giác abc cân a
=> đpcm

Xét ΔABC có \(\widehat{A}=\widehat{B}+\widehat{C}\)
nên ΔABC vuông tại A
Xét ΔABC có
AO là phân giác
CO là phân giác
Do đó: BO là phân giác của góc CBA
\(\widehat{OCB}+\widehat{OBC}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ABC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
nên \(\widehat{BOC}=135^0\)


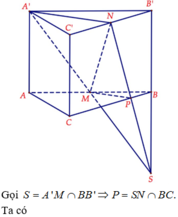
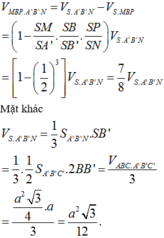
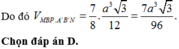
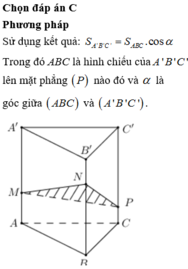

Đáp án là A