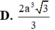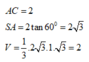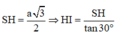Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

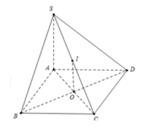
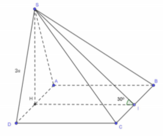
Dễ dàng chứng minh \(BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Gọi O là tâm đáy, kẻ \(OH\perp SC\Rightarrow SC\perp\left(BDH\right)\)
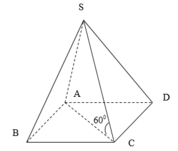
\(\Rightarrow\widehat{BHD}\) hoặc góc bù của nó là góc giữa (SBC) và (SCD) \(\Rightarrow\widehat{BHD}=60^0\) hoặc \(120^0\)
\(\Rightarrow\widehat{BHO}\) bằng \(30^0\) hoặc \(60^0\)
Tam giác ABD đều \(\Rightarrow BD=a\) \(\Rightarrow OB=\dfrac{a}{2}\)
TH1: \(\widehat{BHO}=30^0\)
\(\Rightarrow OH=\dfrac{OB}{tan30^0}=\dfrac{a\sqrt{3}}{2}=OC\Rightarrow\Delta\) vuông OCH có cạnh huyền bằng cạnh góc vuông (loại)
TH2: \(\widehat{BHO}=60^0\Rightarrow OH=\dfrac{OB}{tan60^0}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=AC.\dfrac{OH}{\sqrt{OC^2-OH^2}}=\dfrac{a\sqrt{6}}{4}\)
Từ A kẻ \(AM\perp SB\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(BK;AD\right)=d\left(AD;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)=AM\)
\(\dfrac{1}{AM^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{11}{3a^2}\Rightarrow AM=\dfrac{a\sqrt{33}}{11}\)

Chọn đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó OI ⊥ (ABCD)
⇒ IA = IB = IC = ID với ∆ S A C vuông tại A, IA = IS = IC. Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra IA = a 2 ⇒ SC = 2a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng (ABCD).
![]()
Suy ra ∆ S A C vuông cân
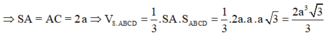
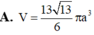
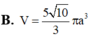
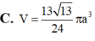
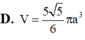






 . Tính
. Tính 

 .
. . Tính
. Tính  bằng:
bằng:
 bằng:
bằng:

 .
.