PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
3
TT
20 tháng 7 2018
Trong năm 2013 , một gia đình có tổng thu nhập 200 triệu đồng . Đến năm 2014 gia đình đó có thêm 1 người nên mặc dù tổng thu nhập tăng thêm 20 triệu đồng nhưng thu nhập tính bình 1 quân theo đầu người lại giảm đi 6 triệu đồng so với năm 2013. Hỏi năm 2014, gia đình đó có bao nhiêu người ? giúp mình với ạ
13 tháng 5 2022
a: Trên hình có 3 góc, đó là các góc xOy;yOz; xOz
b: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\)
nên tia Oy nằm giữa hai tia Ox và Oz
mà \(\widehat{xOy}=\dfrac{1}{2}\widehat{xOz}\)
nên Oy là phân giác của góc xOz
c: \(\widehat{zOx'}=180^0-120^0=60^0\)
SG
1
18 tháng 5 2022
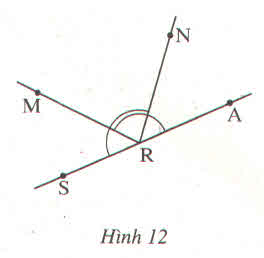
b: \(\widehat{MRS}=180^0-130^0=50^0\)
\(\widehat{ARN}=180^0-130^0=50^0\)
\(\widehat{MRN}=180^0-50^0-50^0=80^0\)
. ai làm được mình sẽ tick.10 lần
5 tháng 8 2016
Ta có định lí :
Một điểm trên một đường thẳng thì có hai tia đối nhau.
Vậy theo đề bài ta có :
5 . 2 = 10 (cặp)
SG
5
4 tháng 5 2017
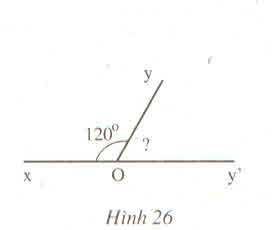
ta có : xOy va yOy' la hai goc ke nhau
=) xOy = 180 do
=> yOy' + xOy = xOy'
=> yOy' = xOy' - xOy =180 - 120 = 60 do
vay yOy' = 60 do
NL
17 tháng 5 2017
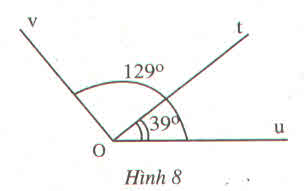
Theo hình vẽ, ta có: \(\widehat{uOt}+\widehat{tOv}=\widehat{uOv}\\ =>\widehat{tOv}=\widehat{uOv}-\widehat{uOt}\\ \widehat{tOv}=129^o-39^o=90^o\)
Với: \(\widehat{tOv}=90^o\)
=> \(\widehat{tOv}\) là góc vuông
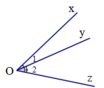
Các góc có trên hình vẽ là xOy ^ , xOz ^ , yOz ^ .