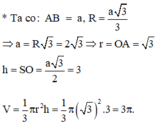Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

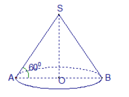
THeo đề bài, đường kính của hình tròn đáy của nón bằng 2a. Vậy bán kính R = a.
Chiều cao của hình nón bằng chiều cao của tam giác đều, nên h = a√3 và
đường sinh l = = 2a.
Vậy diện tích xung quanh của hình nón là:
Sxq = πRl = 2a2π ( đơn vị diện tích).
Thể tích khối nón là:
.
Câu hỏi nào của Võ Nguyễn Thái cũng có Võ Đoong Anh Tuấn làm,có khúc mắc

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

a)Ta xét trong tam giác ABH có Góc H =90độ
=>BAHˆ+ABHˆ=90
mà BAHˆ+HACˆ=90=A^(gt)
=>ABHˆ=HACˆ
Xét tam giác BHA và Tam giác AIC có:
AB=AC(gt)
H^=AICˆ=90(gt)
ABHˆ=HACˆ(c/m trên)
=>Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn)
=>BH=AI(hai cạnh tương ứng)
b)Vì Tam giác BHA=Tam giác AIC(c/m trên)
=>IC=AH(hai cạnh tương ứng)
Xét trong tam giác vuông ABH có:
BH2+AH2=AB2
mà IC=AH
=>BH2+IC2=AB2(th này là D nằm giữa B và M)
Ta có thể c/m tiếp rằng D nằm giữa M và C thì ta vẫn c/m được Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn) và BH2+IC2=AC2=AB2
=>BH2+CI2 có giá trị ko đổi
c)Ta xét trong tam giác DAC có IC,AM là 2 đường cao và cắt nhau tại N(AM cũng là đường cao do là trung tuyến của tam giác cân xuất phát từ đỉnh và cũng chính là đường cao của đỉnh đó xuống cạnh đáy=>AM vuông góc với DC)
=>DN chính là đường cao còn lại=>DN vuông góc với AC(là cạnh đối diện đỉnh đó)
d)Ta dễ dàng tính được Tam giác DMN cân tại M=>DM=MN(dựa vào số đo của các góc và 1 số c/m trên)
Từ M kẻ đường thẳng ME vuông góc với AD còn MF vuông góc với IC,Ta dễ dàng c/m được tam giác MED=Tam giác MFN(cạnh huyền-góc nhọn)
=>ME=MF(là hai đường vuông góc tại điểm M gióng xuống hai cạnh của góc HICˆ)
Theo tính chất của đường phân giác(Điểm nằm trên đường phân giác của góc này thì cách đều hai cạnh tạo thành góc đó)=>IM là tia phân giác của HICˆ

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)