Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có S C D ∩ A B C D = C D
C D ⊥ S A C D ⊥ A C ⇒ C D ⊥ S A C ⇒ S C ⊥ C D
Vì S C ⊥ C D , S C ⊂ S C D A C ⊥ C D , A C ⊂ A B C D
Nên S C D , A B C D ^ = S C A ^ = 45 o
Dễ thấy ∆ S A C vuông cân tại A
Suy ra SA = AC = a 2
Lại có
S M C D = 1 2 M C . M D = 1 2 a . a = a 2 2
Do đó
V = V S . M C D = 1 3 S M C D S A = 1 3 . a 2 2 . a 2 = a 3 2 6
Ta có
B D ∥ M N M N ⊂ S M N ⇒ B D ∥ S M N
Khi đó d( SM,BD ) = d( SM, (SMN) ) = d( D, (SMN) ) = d( A, ( SMN) )
Kẻ A P ⊥ M N , P ∈ M N A H ⊥ S P , H ∈ S P
Suy ra A H ⊥ S M N ⇒ d A S M N = A H
∆ S A P vuông tại A có
1 A H 2 = 1 S A 2 + 1 A P 2 = 1 S A 2 + 1 A N 2 + 1 A M 2 = 1 2 a 2 + 1 a 2 4 + 1 a 2 = 11 2 a 2
Do đó d = d( SM, BD ) = AH = a 22 11
Đáp án A

Đáp án D
Vì A, B, C lần lượt là hình chiếu vuông góc của M trên trục Ox, Oy, Oz nên: A − 3 ; 0 ; 0 B 0 ; 2 ; 0 C 0 ; 0 ; 4

Em có M’ là hình chiếu song song của M trên (ABC)
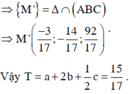

Đáp án D
Vì A, B, C lần lượt là hình chiếu vuông góc của M trên trục Ox, Oy, Oz nên: A − 3 ; 0 ; 0 B 0 ; 2 ; 0 C 0 ; 0 ; 4

Em có M’ là hình chiếu song song của M trên (ABC)
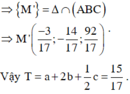

Phương pháp:
- Gắn hệ tọa độ Oxyz với O là tâm hình vuông đáy,

- Xác định tọa độ các điểm cần thiết và tính khoảng cách.
Cách giải:
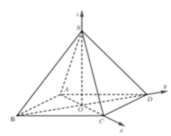
Gắn hệ trục tọa độ như hình vẽ, giả sử SO = b ta có:
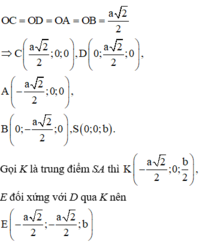

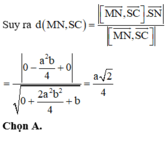

Đáp án là C.
Không mất tính tổng quát, giả sử
x C > x B .
Ta có: d có phương trình
y = m x − 2 .
Phương trình hoành độ giao điểm:
m x − 2 = − x 3 + 6 x 2 − 9 x + 2
⇔ x = 2 x 2 − 4 x + 1 + m = 0
Để tồn tại A, B, thì phương trình x 2 − 4 x + m + 1 = 0 phải có 2 nghiệm phân biệt khác 2
⇔ m < 3 ⇒ x A = 2 ; x B + x C = 4 ; x B x C = m + 1 ; y C − y B = m x C − x B .
Trường hợp 1: ⇒ x B x C = m + 1 > 0 ⇔ − 1 < m < 3 * .
Ta có .
S B B ' C ' C = B B ' + C C ' . B ' C ' 2 = x B + x C . m x C − x B 2 = 8 ⇔ 4 m 16 − 4 m + 1 2 = 8
.
Đối chiếu điều kiện (*) ta được m=2.
Trường hợp 2:
x C > 0 > x B ⇒ x B x C = m + 1 < 0 ⇔ m < − 1 < 0
(Loại vì m > 0 ).



Đáp án A
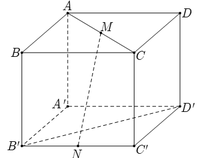
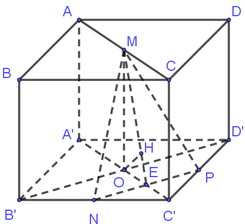
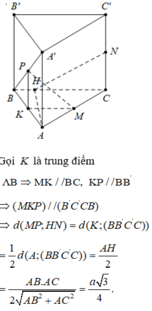
Qua N vẽ EK song song với A D E ∈ A B , K ∈ D C .
Qua M vẽ MQ song song với A ' D ' Q ∈ D ' C '
Ta có A A ' D ' D / / E M Q K ,mà H P ⊂ A A ' D ' D , M N ⊂ E M Q K nên
d M N , H P = d A A ' D ' D , E M Q K = 1 2 d A ' A D D ' , B ' B C C ' = 1 2 B H = 1 2 a 3 2 = a 3 4 .