Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
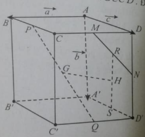
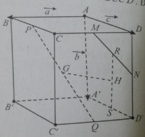
a) Tứ giác DBB'D' là hình bình hành nên BD // B'D' . Vì vậy BD // (B'D'C) và BA' // CD' \(\Rightarrow\) BA' // ( B'D'C).
Từ đó suy ra ( BDA') //B'D'C).
b) Gọi ,
là giao điểm của AC' với A'O và CO'.
Do \(G_1=A'O\cap AI\) và A'O và AI là hai đường trung tuyến của tam giác nên \(G_1\) là trọng tâm của tam giác A'AC.
Chứng minh tương tự \(G_2\) là trọng tâm tam giác CAC'.
Suy ra \(\dfrac{AG_1}{AO}=\dfrac{2}{3}\); \(\dfrac{CG_2}{CO}=\dfrac{2}{3}\) nên đường chéo AC' đi qua trọng tâm của hai tam giác BDA' và B'D'C.
c) Do O và O' lần lượt là trung điểm của AC và A'C' nên \(OC=A'O'\) và OC' // A'O'.
Vì vậy tứ giác OCO'A là hình bình hành và OA'//OC.
Từ đó ta chứng minh được \(G_1\) lần lượt là trung điểm của \(AG_1\) và \(G_2\) là trung điểm của \(G_1C'\).
Do đó: \(AG_1=G_1G_2=G_2C\) (đpcm).
d) \(\left(A'IO\right)=\left(AA'C'C\right)\). Nên thiết diện cần tìm là (AA'C'C).

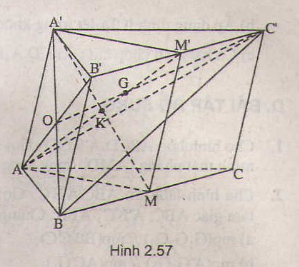
a) Do MM' lần lượt là trung điểm của BC và B'C' nên M'M//BB'//CC'. Vì vậy MM'//AA'.
Vì vậy tứ giác A'M'MA là hình bình hành. Suy ra: AM//A'M'.
b) Trong mp (AA'M'M), ta có: MA' ∩ AM' = K.
Do \(K\in A'M\) và \(A'M\in\left(AB'C'\right)\) nên K (AB'C').
c) Có \(O=AB'\cap A'B\) nên \(O\in\left(AB'C'\right)\cap\left(BA'C'\right)\).
Suy ra: \(d\equiv CO'\).
d) Trong (AB'C'): C'O ∩ AM' = G vì vậy G ( AMM') . Mà O, M' lần lượt là trung điểm AB' và B'C' nên G là trọng tâm của tam giác AB'C'.



Đáp án C