Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)

a) Áp dụng định lí Pytago vào ΔAEC vuông tại E, ta được:
\(AC^2=AE^2+EC^2\)
\(\Leftrightarrow EC^2=AC^2-AE^2=5^2-4^2=9\)
hay EC=3(cm)
Vậy: EC=3cm
Ta có: BE+EC=BC(E nằm giữa B và C)
nên BE=BC-EC=9-3=6(cm)
Vậy: BE=6cm
Áp dụng định lí Pytago vào ΔABE vuông tại E, ta được:
\(AB^2=AE^2+BE^2\)
\(\Leftrightarrow AB^2=6^2+4^2=52\)
hay \(AB=2\sqrt{13}cm\)
Vậy: \(AB=2\sqrt{13}cm\)
b) Chu vi của tam giác ABC là:
\(AB+AC+BC=2\sqrt{13}+5+9=14+2\sqrt{13}cm\)

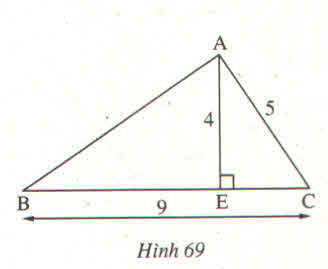
Áp dụng định lý pitago vào tam giác vuông AEC ta có:
AC2=AE2+EC2
=>EC2=AC2-AE2=52-42=25-16=9
=>EC=3M
Ta có: BC = BE + EC
BE = BC – EC = 9 – 3 = 6(m)
Áp dụng định lí pitago vào tam giác vuông AEB, ta có:
AB2=AE2+EB2=42+62=16+36=52
Suy ra: AB = √52(m) ≈7,2m