K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
18 tháng 3 2018
Chọn D.
Phương pháp:
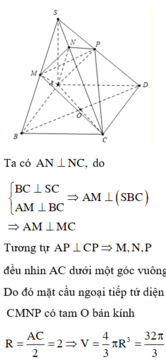
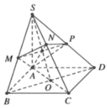
+ Chứng minh: O là tâm mặt cầu ngoại tiếp tứ diện CMNP (với O là tâm của hình vuông ABCD)



10 tháng 10 2015
hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m



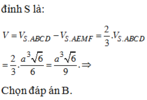
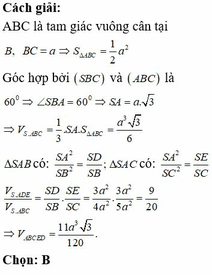

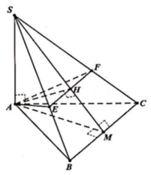

Đáp án B
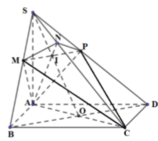
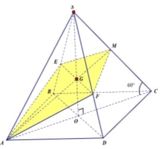
Nối S O ∩ A N = E , qua E kẻ đường thẳng song song với BD. Cắt SB,SD lần lượt tại M , P ⇒ m p P ≡ A M N P .
Ta có S A ⊥ A B , S A ⊥ A D ⇒ S A ⊥ A B C D ⇒ B C ⊥ S A B .
Mà SC ⊥ A M N P ⇒ S C ⊥ A M suy ra A M ⊥ S B C .
Do đó A M ⊥ M C mà O là trung điểm của A C ⇒ O A = O M = O C .
Tương tự, ta chứng minh được O là tâm mặt cầu ngoại tiếp khối
đa diện A B C D . M N P ⇒ R = A C 2 = 4 a 3 2 = 2 a 3 .
Vậy thể tích cần tính là V = 4 3 π R 3 = 4 3 π 2 3 3 = 32 3 π a 3 .