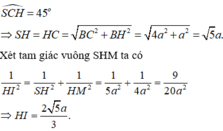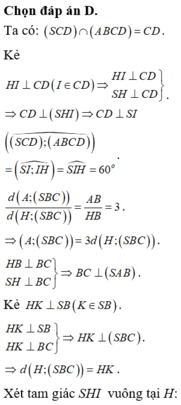Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

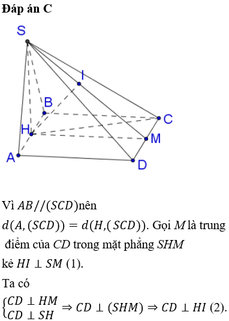
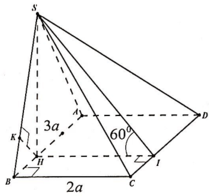
Gọi M là trung điểm CD, P là hình chiếu của H lên SM khi đó H M ⊥ C D ; C D ⊥ S H mà H P ⊥ S M ⇒ H P ⊥ S C D . Lại có A B / / C D suy ra A B / / S C D ⇒ d A ; S C D = d H ; S C D = H P
Ta có 1 H P 2 = 1 H M 2 + 1 H S 2 suy ra H P = a 6 3
Vậy d A ; S C D = a 6 3
Đáp án A

Đáp án C

Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có: C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ ( S H M ) ⇒ ⊥ H K
Mặt khác ta có H K ⊥ S M
Suy ra H K ⊥ ( S C D )
Vậy d ( A , ( S C D ) ) = D ( H , ( S C D ) ) = H K
Xét tam giác BHC vuông tại B, ta có:
H C = B H 2 + B C 2 = a 2 ⇒ S H = H C = a 2
Xét tam giác SHM vuông tại H, ta có:
1 H K 2 = 1 S H 2 + 1 M H 2 = 1 2 a 2 + 1 a 2 = 3 2 a 2 ⇒ H K = a 6 3

Đáp án C
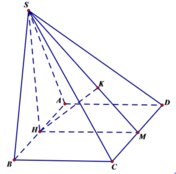
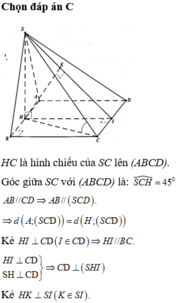
Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có: C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ ( S H M ) ⇒ ⊥ H K
Mặt khác ta có H K ⊥ ( S C D )
Suy ra H K ⊥ ( S C D )
Vậy d ( A , ( S C D ) ) = D ( H , ( S C D ) ) = H K
Xét tam giác BHC vuông tại B, ta có:
H C = B H 2 + B C 2 = a 2 ⇒ S H = H C = a 2
Xét tam giác SHM vuông tại H, ta có:
1 H K 2 = 1 S H 2 + 1 M H 2 = 1 2 a 2 + 1 a 2 = 3 2 a 2 ⇒ H K = a 6 3

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Đáp án B
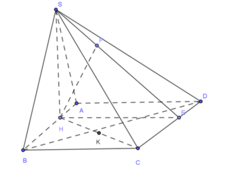
d K , S C D = 1 2 d H , S C D = 1 2 H F .
A H = 1 3 A B = 1 3 a ; B H = 2 3 A B = 2 3 a
C H = B H 2 + B C 2 = 13 3 a .
C ó g ó c g i ữ a S C v à đ á y l à 60 ° n ê n t a c ó
S C H ^ = 60 0 ⇒ S H = tan 60 0 . C H = 39 3 a
ta có 1 H F 2 = 1 H E 2 + 1 A H 2 ⇒ H F = 13 4 a

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2