Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S B N M C D I K A
Gọi I là trung điểm của đoạn AB \(\Rightarrow SI\perp AB,\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SI\perp\left(ABCD\right)\)
Nên \(\widehat{SCI}=\left(\widehat{SC,\left(ABCD\right)}\right)=60^0,CI=\frac{a\sqrt{3}}{2}\Rightarrow SI=CI\tan60^0=\frac{3a}{2}\)
Gọi M là trung điểm của đoạn BC, N là trung điểm đoạn BM
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow IN=\frac{a\sqrt{3}}{4}\)
Ta có : \(S_{ABCD}=2S_{\Delta ABC}=\frac{a^2\sqrt{3}}{2}\Rightarrow V_{S.ABCD}=\frac{1}{3}.\frac{a^2\sqrt{3}}{2}.\frac{3a}{2}=\frac{a^2\sqrt{3}}{4}\)
Ta có \(BC\perp IN,BC\perp SI\Rightarrow BC\perp\left(SIN\right)\)
Trong mặt phẳng (SIN) kẻ \(IK\perp\left(SN\right),K\in SN\), ta có :
\(\begin{cases}IK\perp SN\\IK\perp BC\end{cases}\) \(\Rightarrow IK\perp\left(SBC\right)\Rightarrow d\left(I,\left(SBC\right)\right)=IK\)
Lại có :
\(\frac{1}{IK^2}=\frac{1}{IS^2}+\frac{1}{IN^2}\Rightarrow IK=\frac{3a\sqrt{13}}{26}\Rightarrow d\left(I,\left(SBC\right)\right)=\frac{3a\sqrt{13}}{26}\)
\(\Rightarrow d\left(A,\left(SBC\right)\right)=\frac{3a\sqrt{13}}{13}\)


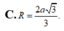
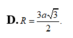


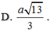
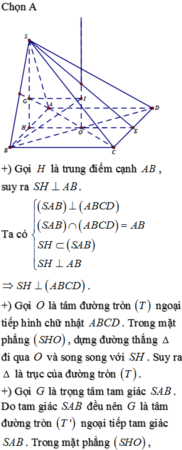


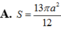
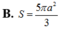

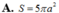

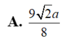
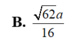
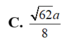
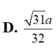
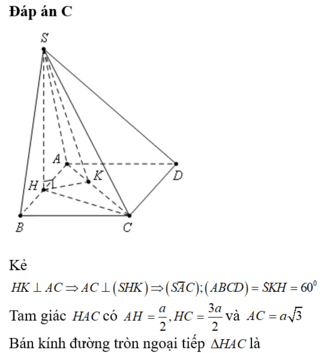

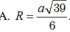
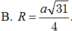
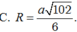
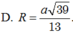

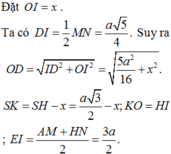
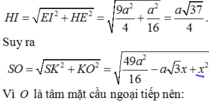
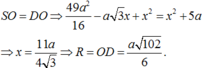
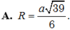
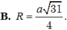
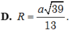

Đáp án D
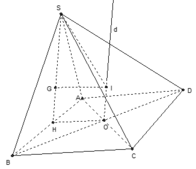
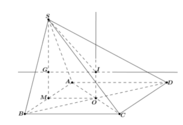
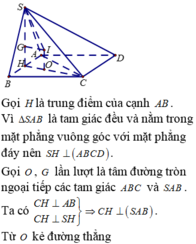
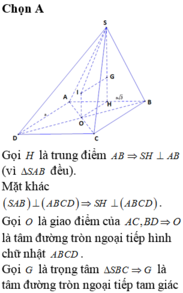
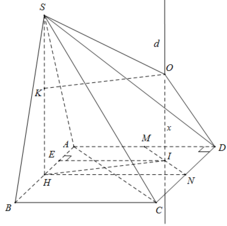
Gọi H là trung điểm của AB, do tam giác SAB đều nên SH ⊥ AB mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD)
Gọi O là tâm của hình vuông ABCD, d là đường thẳng qua O và song song SH thì d ⊥ (ABCD) hay d là trục đường tròn ngoại tiếp hình vuông ABCD
Trong mặt phẳng (SAB) từ G kẻ đường thẳng vuông góc với (SAB) cắt d tại I thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính R = IS.