Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
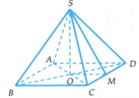
Gọi O là tâm của hình vuông ABCD, suy ra S O ⊥ A B C D
Gọi M là trung điểm của CD thì C D ⊥ O M mà C D ⊥ O M ⇒ C D ⊥ S O M
![]()
![]()
Đặt AB = 2x(x > 0) ⇒ O M = x
![]()
Do ∆ S O M vuông tại O nên S O = O M . tan S M O ⏜ = x . tan α
Do ∆ S O A vuông tại O nên S A 2 = S O 2 + O A 2
![]()
![]()
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 S O . S A B C D
Ta có
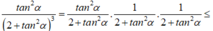
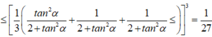
Suy ra 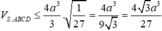
Dấu “=” xảy ra khi
![]()
![]()

Chọn B.
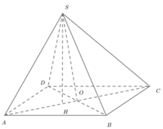
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.



Chọn đáp án A
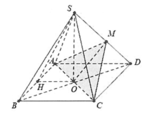
Gọi O là tâm hình vuông ABCD, H là trung điểm của AB
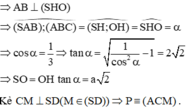
Mặt phẳng (ACM) chia khối chóp S.ABCD thành hai khối đa diện M.ACD có thể tích V1 và khối đa diện còn lại có thể tích V2

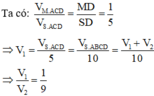

Đáp án A.
Gọi O là tâm hình vuông ABCD, H là trung điểm AB.
⇒ A B ⊥ S H O ⇒ S A B ; A B C D ^ = S H ; O H ^ = S H O ^ = α . ⇒ c o s α = 1 3 ⇒ tan α = 3 x 2 − 1 = 2 2 ⇒ S O = tan α × O H = a 2 .
Kẻ CM vuông góc với SD M ∈ S D ⇒ m p P ≡ m p A C M .
Mặt phẳng A M C chia khối chóp A.ABCD thành hai khối đa diện gồm M.ACD có thể tích là V 1 và khối đa diện còn lại có thể tích V 2 .
Diện tích tam giác SAB là S Δ S A B = 1 2 . S H . A B = a 2 . 3 a 2 = 3 a 2 4 .
Và
S D = S O 2 + D O 2 = a 10 2 ⇒ S Δ . S C D = 1 2 . S H . S D ⇒ C M = 3 a 10 .
Tam giác MCD vuông tại M ⇒ M D = C D 2 − M C 2 = a 10 ⇒ M D S D = 1 5 .
Ta có:
V M . A C D V S . A C D = M D S D = 1 5 ⇒ V M . A C D = V S . A B C D 10 ⇔ V 1 = V 1 + V 2 10 ⇔ V 1 V 2 = 1 9 .

Đáp án A
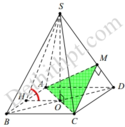
Gọi I,J lần lượt là trung điểm cạnh BC và SA
Ta có A C ⊥ S B D , EI // AC, MJ//AC => E I ⊥ ( S B D ) , M J ⊥ ( S B D )
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
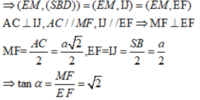
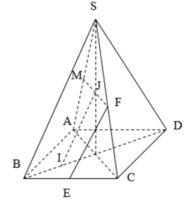

Đáp án C
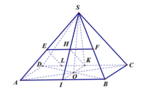
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
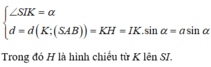

Đáp án C
Phương pháp:
- Gắn hệ trục tọa độ Oxyz, tìm tọa độ các điểm E, M.
- Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin α = n → . u → n → . u →
Cách giải:
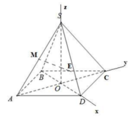
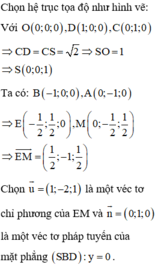
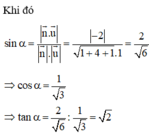
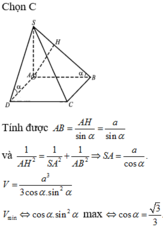

Chọn D
H là tâm đường tròn nội tiếp đáy.
Cách giải: Vì góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α nên H là tâm đường tròn nội tiếp ABCD.
Vì các cạnh bên hình chóp S.ABCD bằng a nên H là tâm đường tròn ngoại tiếp ABCD.
Vậy ABCD là hình vuông. Suy ra S.ABCD là hình chóp tứ giác đều.