Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

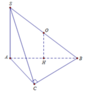
Đáp án D
Vì B C ⊥ S A B C ⊥ C A ⇒ B C ⊥ S A C ⇒ B C ⊥ S C ⇒ O là tâm đường tròn ngoại tiếp tam giác SBC
Vì S A ⊥ A B C ⇒ H là trung điểm của AB

∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
B A C M
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = 1/2 BC
Vì G là trọng tâm của ∆ ABC nên AG = 2/3 AM AM => AG = 2/3.1/2 BC
=> AG = 1/3 BC = 1/3.5 = 1.7cm

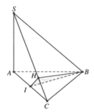
Gọi I là giao điểm của phân giác góc B và C
Xét tam giác HAC vuông tại H và tam giác ABC vuông tại A có góc C chung => góc HAC = góc ABC
Ta có: góc ADC = góc DAB + góc DBA = góc DAH + góc HAC ( vì góc DAB = DAH ; góc HAC=DBA)
=>góc ADC= góc DAH + góc HAC = góc DAC
=> tam giác CAD cân tại C => CA=CD
tam giác CID = tam giác CIA (c.g.c) => IA = ID (1)
CM tương tự, ta có IA = IE (2)
Từ (1) và (2) suy ra IA = IE = ID => I là giao điểm 3 đường trung trực của tam giác ADE
=> đpcm

Đáp án A
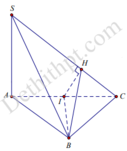
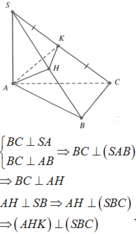
Vì Δ A B C cân tại B nên I là trung điểm của AC nên B I ⊥ A C .
Ta có:
S A ⊥ B I , B I ⊥ A C ⇒ B I ⊥ S A C ⇒ B I ⊥ S C
mà
S C ⊥ I H ⇒ S C ⊥ B I H ⇒ S B C ⊥ B I H .
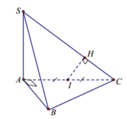
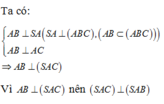



Đáp án A
Phương pháp:
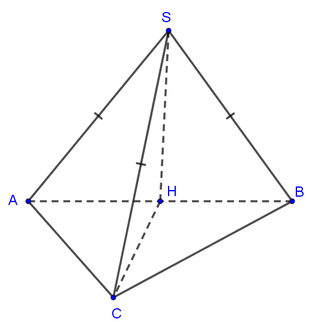
Gọi M là trung điểm của AB, chứng minh S M ⊥ A B C bằng cách sử dụng tính chất của trục đường tròn đáy.
Cách giải: Gọi M là trung điểm của AB.
Vì Δ A B C vuông tại C nên M A = M B = M C . .
Mà S A = S B = S C nên SM là trục đường tròn ngoại tiếp tam giác ABC.
Suy ra S M ⊥ A B C .
Vậy H ≡ M là trung điểm của AB.
Chú ý khi giải: Cần tránh nhầm lẫn với trường hợp chóp tam giác đều: HS dễ nhầm lẫn khi nghĩ rằng S A = S B = S C thì hình chiếu vuông góc của S sẽ là trọng tâm tam giác dẫn đến chọn nhầm đáp án B.