Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Ta có :
Góc BAD + ADC = 180o
=> \(\frac{1}{2}gocBAD+\frac{1}{2}gocADC=\frac{1}{2}.180^o\)
=> \(gocMAD+gocMDA=90^o\)
=> Xét \(\Delta MAD\)có \(gocMAD+gocMDA=90^o\Rightarrow gocAMD=90^o\)
=> Sử dụng góc kề bù ta suy ra \(gocAMD=gocAMF=gocDME=90^o\)
Xét \(\Delta AMD=\Delta AMF\left(g.c.g\right)\)
\(gocDAM=gocFAM\)( AE là phân giác góc A )
Chung cạnh AM
\(gocAMD=gocAMF\left(cmt\right)\)
=> \(\Delta AMD=\Delta AMF\left(g.c.g\right)\)
=> M là trung điểm DF
Tớ chỉ làm được tới đây

Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B
- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc Bnhuquynhdat, 17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg

Tứ giác ABCD có A^+B^+C^+D^=360độ
D^+C^=150độ
\(\frac{1}{2}\)D^+\(\frac{1}{2}\)C^=\(\frac{150}{2}\)độ
\(\Rightarrow\)D2^+C2^=\(\frac{150}{2}\)=75độ
Tam giác DEC có D2^+C2^+CED^=180độ
CED^=105độ

a, góc FAD + góc DAE = 90
góc BAE + góc DAE = 90
=> góc FAD = góc BAE
xét tam giác ADF và tam giác ABE có : góc ADF = góc ABE = 90
AD = AB do ABCD là hình vuông (gt)
=> tam giác ADF = tam giác ABE (cgv-gnk)
=> AF = AE (đn)
=> tam giác AFE cân tại A (đn)
góc AFE = 90 (gT)
=> tam giác AFE vuông cân (dh)
b, tam giác AFE cân tại A (câu a)
AI Là trung tuyến của tam giác AFE (gt)
=> AI _|_ FE (đl) (1)
EG // AB (gt)
AB // DC do ABCD là hình vuông (gT)
=> EG // FK (2)
=> góc GEI = góc IFK (slt)
xét tam giác GIE và tam giác KIF có : góc GIE = góc KIF (đối đỉnh)
FI = IE do I là trđ của FE (gt)
=> tam giác GIE = tam giác KIF (g-c-g)
=> GE = FK (3)
(2)(3) => GEFK là hình bình hành và (1)
=> GEFK là hình thoi (dh)

d) chứng minh được tam giác AIE = tam giác DIC (có dữ kiện đầy đủ rồi)
tam giác ACD = tam giác FCB (chứng minh được luông)
=> Sacd = S fcb
Ta có:
S ABD = 1/2 S ABCD (tam giác ABD = tam giác FBD)
=> S BAC + S ACI + S CID = 1/2 S ABCD
=> S BAC + SACI + S AIE = 1/2 S ABCD (tam giác AID = tam giác AIE => S AID = S AIE)
mà S BAC + SACI + S AIE = S ABCE
=> S ABCE = 1/2 S ABCD (đpcm)
p/s: có chỗ nào không hiểu thì cứ nhắn tin hỏi ~
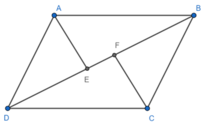


Ta có S A B C F E = S A B E + S B F C S A D C F E = S D F C + S D A E
Xét hình bình hàng ABCD có AE và CF lần lượt là phân giác của các góc A và C
nên suy ra: B A E ^ = D A E ^ = B C F ^ = D C F ^
Xét ΔABE và ΔDCF có:
AB = CD (gt), A B E ^ = C D F ^ (slt), B A E ^ = D C F ^ (cmt)
=> ΔABE = ΔDCF (g.c.g)
=> SABE = SCDF (1)
Xét ΔBCF và ΔDAE có:
AD = BC (gt), A D E ^ = C B F ^ (slt), D A E ^ = B C F ^ (cmt)
=> ΔBCF = ΔDAE (g.c.g)
=> SBCF = SDAE (2)
Từ (1) và (2) suy ra:
SABE + SBCF = SCDF + SDAE
=> SABCFE = SADCFE
Đáp án cần chọn là: C