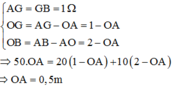Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
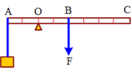
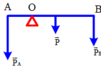
P = m g = 2.10 = 20 ( N ) ; P A = m A . g = 5.10 = 50 ( N ) ; P B = m B . g = 1.10 = 10 ( N )
Theo điều kiện cân bằng Momen lực: MA = MP + MB
⇒ P A . O A = P . O G + P B . O B
AG = GB = 1m
OG = AG – OA = 1 – OA
OB = AB – AO = 2 – OA
=> 50. OA = 20 (1- OA) + 10( 2 – OA )
=> OA = 0,5m
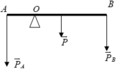

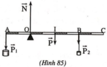
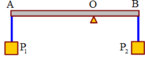
a/ Tổng tất cả các lực t/d= 100+300=400(N)
b/ Khối lượng của thanh sẽ t/d lên trung điểm của thanh, ta nhận thấy Pa<Pb \(\Rightarrow P_A.d_A+P.d=P_B.d_B\Leftrightarrow100.\left(\dfrac{AB}{2}+d\right)+5000.d=300.\left(\dfrac{AB}{2}-d\right)\)
(d là khoảng cách giữa trọng tâm thanh đến điểm tựa)
Từ đó bạn tìm được d

\(OB=1,2m\)
\(\Rightarrow OA=1,5-1,2=0,3m\)
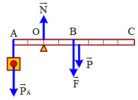
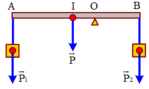
Để AB cân bằng \(\Leftrightarrow M_A=M_B\)
\(\Rightarrow m_1g\cdot OA=m_2g\cdot OB\)
\(\Rightarrow\dfrac{P_1}{10}\cdot OA=\dfrac{P_2}{10}\cdot OB\)
\(\Rightarrow\dfrac{P_1}{10}\cdot0,3=\dfrac{50}{10}\cdot1,2\)
\(\Rightarrow P_1=200N\)

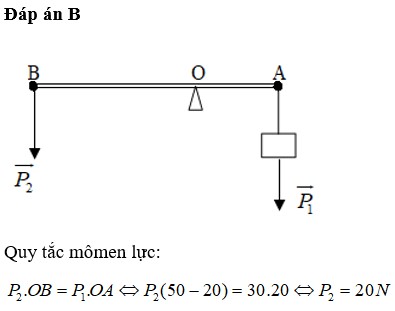
\(OA=40cm=0,4m\)
\(\Rightarrow OB=AB-OA=1,2-0,4=0,8m\)
Để AB cân bằng thì: \(M_A=M_B\)
\(\Rightarrow m_1\cdot g\cdot OA=m_2\cdot g\cdot OB\)
\(\Rightarrow\dfrac{P_1}{10}\cdot OA=\dfrac{P_2}{10}\cdot OB\)
\(\Rightarrow\dfrac{40}{10}\cdot0,4=\dfrac{P_2}{10}\cdot0,8\)
\(\Rightarrow P_2=20N\)