Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

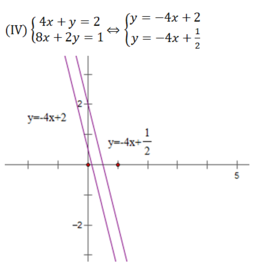
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
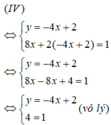
Vậy hệ phương trình (IV) vô nghiệm.

a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :
\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)
b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)
Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)
Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)
P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))

1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)

\(\hept{\begin{cases}x-my=1\\mx+y=1\end{cases}}\)
<=> \(\hept{\begin{cases}mx-m^2y=m\\mx+y=1\end{cases}}\)
<=> \(\hept{\begin{cases}x-my=1\\\left(1+m^2\right)y=1-m\end{cases}}\)
<=> \(\hept{\begin{cases}x=1+my\\y=\frac{1-m}{m^2+1}\end{cases}}\)
<=> \(\hept{\begin{cases}x=1+m.\frac{1-m}{m^2+1}=\frac{1+m}{m^2+1}\\y=\frac{1-m}{m^2+1}\end{cases}}\)
Vậy với mọi m hệ luôn có nghiệm duy nhất.
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
Vậy hệ phương trình (IV) vô nghiệm.