Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sau mỗi nửa chu kì, biên độ của con lắc giảm là:
\(2\dfrac{\mu.mg}{k}=2\dfrac{0,01.0,1.10}{100}=0,0001m=0,1mm.\)
Sau mỗi lần vật qua VTCB thì đúng bằng nửa chu kì, do đó biên độ dao động giảm là 0,1 mm.

A B 0 5cm -5cm 3cm
Áp dụng định luật bảo toàn năng lượng
Vật đi từ A được 2 cm tức là vật đang có li độ x = 3 cm.
\(W_{A,x=5cm } = W_{B,x=3cm}\)
=> \(\frac{1}{2}kx_0^2 = A_{F_{ms}}+\frac{1}{2}mv_1^2+\frac{1}{2}kx_1^2\)
=> \(\frac{1}{2}k(x_0^2-x_1^2) = F_{ms}S+\frac{1}{2}mv_1^2\)
=>\(\frac{1}{2}mv_1^2= \frac{1}{2}k(x_0^2-x_1^2) - \mu mgS\)
=>\(\frac{1}{2}mv_1^2= \frac{1}{2}100(0,05^2-0,03^2) - 0,25.1. 10. 0,02\)
=> \(\frac{1}{2}mv^2 = 0,03\)
=> \(v = \sqrt{\frac{2.0,03}{1}} = 0,245 m/s.\)
Mình nghĩ là kết quả là 0,245 m/s.

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

Độ giãn của lò xo tại VTCB: \(\Delta l_0=\frac{9}{\omega^2}=2cm\)
Lực đàn hồi có độ lớn 1,5 N
\(F=k.\left(\Delta l\pm x\right)\Leftrightarrow1,5=50.\left(0,02\pm x\right)\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=1cm\\x=-1cm\end{array}\right.\)
Khoảng thời gian ngắn nhất vật đi qua hai vị trí mà lực đàn hồi F = 1,5 N là :
\(t=\frac{T}{12}+\frac{T}{12}=\frac{\pi}{30\sqrt{5}}=s\)
Đáp án C

Ở VTCB lò xo dãn: \(\Delta \ell_0=10cm\)
Tần số góc: \(\omega=\sqrt{\dfrac{g}{\Delta\ell_0}}=10(rad/s)\)
Áp dụng công thức: \(v_0^2=v^2+\dfrac{a^2}{\omega^2}\)
\(\Rightarrow v_0^2=20^2+\dfrac{(200\sqrt 3)^2}{10^2}\)
\(\Rightarrow v_0=40(cm/s)\)
Biên độ dao động: \(A=\dfrac{v_0}{\omega}=4cm\)
Tỉ số giữa lực đàn hồi cực đại và cực tiểu:
\(\dfrac{F_{dhmax}}{F_{dhmin}}=\dfrac{k.(\Delta\ell_0+A)}{k.(\Delta\ell_0-A)}=\dfrac{\Delta\ell_0+A}{\Delta\ell_0-A}=\dfrac{10+4}{10-4}=\dfrac{7}{3}\)

\(A=10cm\)
\(\Rightarrow\omega=5\sqrt{2}\)
\(\Rightarrow A_{max}=A-\frac{umg}{k}=0,08\)
\(\Rightarrow v_{max}=A_{max}\omega=0,4\sqrt{2}\left(\frac{m}{s}\right)\)
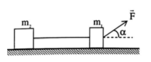

Các lực tác dụng vào hệ như hình vẽ. Áp dụng định luật II Newton cho từng vật ta được:
⇒ a = 10. c o s 30 0 − 0 , 2 0 , 5.10 − 10. sin 30 0 − 0 , 2.1.10 0 , 5 + 1 = 4 , 44 m / s 2