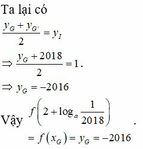Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

Phương trình hoành độ giao điểm của (C) và đường thẳng d:
2 x + 1 x - 1 = x + m ( x ≠ 1 ) ⇔ x 2 + ( m - 3 ) x - m - 1 = 0 ( 1 )
Khi đó cắt (C) tại hai điểm phân biệt A: B khi và chi khi phương trình (1) có hai nghiệm phân biệt khác -1
⇔ ( m - 3 ) 2 + 4 ( m + 1 ) > 0 1 2 + ( m - 3 ) - m - 1 ≠ 0 ⇔ m 2 - 2 m + 13 > 0 - 1 ≠ 0 luôn đúng
Gọi A( x1 ; x1+m) ; B( x2 ; x2+m) trong đó x1 ; x2 là nghiệm của (1) , theo Viet ta có
x 1 + x 2 = 3 - m x 1 x 2 = - m - 1
Gọi I ( x 1 + x 2 2 ; ( x 1 + x 2 + 2 m 2 ) là trung điểm của AB, suy ra I ( 3 - m 2 ; 3 + m 2 ) , nên
C I → ( - 2 - 3 - m 2 ; 5 - 3 + m 2 )
⇒ C I = 1 2 ( m - 7 ) 2 + ( 7 - m ) 2 .
Mặt khác A B → = ( x 2 - x 1 ; x 2 - x 1 )
⇒ A B = 2 ( x 2 - x 1 ) 2 = 2 ( m 2 - 2 m + 13 ) 2
Vậy tam giác ABC đều khi và chỉ khi
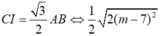
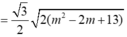
![]()
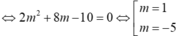

Ta có \(d:y=mx-m-2\)
Hoành độ giao điểm là nghiệm của phương trình :
\(\frac{x-3}{1-x}=mx-m-2\Leftrightarrow\begin{cases}x\ne1\\mx^2-\left(2m+1\right)x+m-1=0\end{cases}\)
Điều kiện để cắt nhau tại hai điểm phân biệt là : \(\begin{cases}m\ne0\\m>-\frac{1}{8}\end{cases}\)
Gọi \(M\left(x_1;y_1\right);N\left(x_2;y_2\right)\) khi đó \(\begin{cases}x_1+x_2=\frac{2m+1}{m}\\x_1x_2=\frac{m-1}{2}\end{cases}\)
Ta có \(\overrightarrow{AM}=-2\overrightarrow{AN}\Rightarrow x_1=3-2x_2\)
Từ đó ta có m = 1

Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
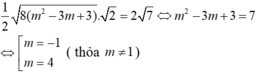
Chọn B.

hoành độ giao điểm là nghiệm của pt
\(\left(x+1\right)\left(1-2x\right)=x+2m\Leftrightarrow-2x^2-x+1=x+2m\Leftrightarrow2x^2+2x+2m-1=0\)(*)
để đồ thị hàm số cắt đt d tại 2 điểm pb A,B thì pt(*) có 2 nghiệm phân biệt
\(\Delta=1-2\left(2m-1\right)=3-4m>0\Leftrightarrow m<\frac{3}{4}\)
vậy với m<3/4 thì đồ thị hàm số cắt d tại 2 điểm pb \(A\left(\frac{-1+\sqrt{3-4m}}{2};\frac{-1+\sqrt{3-4m}}{2}\right)\);\(B\left(\frac{-1-\sqrt{3-4m}}{2};\frac{-1-\sqrt{3-4m}}{2}+2m\right)\)
ta có \(S_{ABI}=\frac{1}{2}AB.d\left(I,d\right)\)
\(d\left(I,d\right)=\frac{\left|1+2m\right|}{\sqrt{2}}\); \(\vec{AB}=\left(-\sqrt{3-4m};-\sqrt{3-4m}\right)\Leftrightarrow AB=\sqrt{2\left(3-4m\right)}=\sqrt{2}.\sqrt{3-4m}\)
\(S_{ABI}=\frac{1}{2}\frac{\left|1+2m\right|}{\sqrt{2}}.\sqrt{2}.\sqrt{3-4m}=\frac{\sqrt{3-4m}\left|1+2m\right|}{2}=1\Leftrightarrow\left|1+2m\right|\sqrt{3-4m}=2\)
bình phương 2 về lên
ta tìm đc m đối chiếu với đk của m ta đc điều cần tìm
\(A\left(\frac{-1+\sqrt{3-4m}}{2};\frac{-1+\sqrt{3-4m}}{2}+2m\right)\)